Optimization
loss를 줄여나가는 학습하는 방법을 총칭해서 이르는 말. 최적화
convex function 형태로 (예측값 - 실제값)^2 나타남
loss를 낮추는 방법 = 학습하는 방법 = 하산법
높은 곳에서 낮은 곳으로 내려오는 것
▪️ Loss-function
우리가 학습 시킨 모델이 얼마나 잘했는지를 정량적으로 수치화하는 것
Loss-function = cost-function = Error
Loss function은 하산법으로 치면 고도, 위치를 알아야 어느 방향으로 최적으로 내려갈지 결정할 수 있음, 현재 loss를 바탕으로 가장 가파르게 내려갈 수 있게끔 계산함 ⇒ Backpropagation (미분, 편미분 개념)
▪️ Backpropagation 방법으로 내려가는 optimization의 종류가 Gradient Descent

▪️Gradient Descent
가장 가파르게 Loss를 감소하는 W 방향을 수학적으로 계산(편미분)한 뒤, 해당 방향으로 이동
→ 가장 가파르게 내려갈 수 있는 방향을 계산해서 해당 방향으로 한 발짝 이동

⇒ NeuralNet 기반의 학습에 있어서 중요한 역할!
학습은 propagation과 관련 없고, Backward와 관련됨
loss가 나온다는 것은 수치적으로 얼마나 잘 예측했느냐 이다.
고도가 나오면 고도를 중심으로 loss를 최소화 시키면서 진행하는 backpropagation
딥러닝에서의 학습은 Weight 값을 수정하는 일과 같다.
다시 loss 최소화 시키며 돌아가서 보정 된 Weight 를 적용시키는 과정을 반복한다.
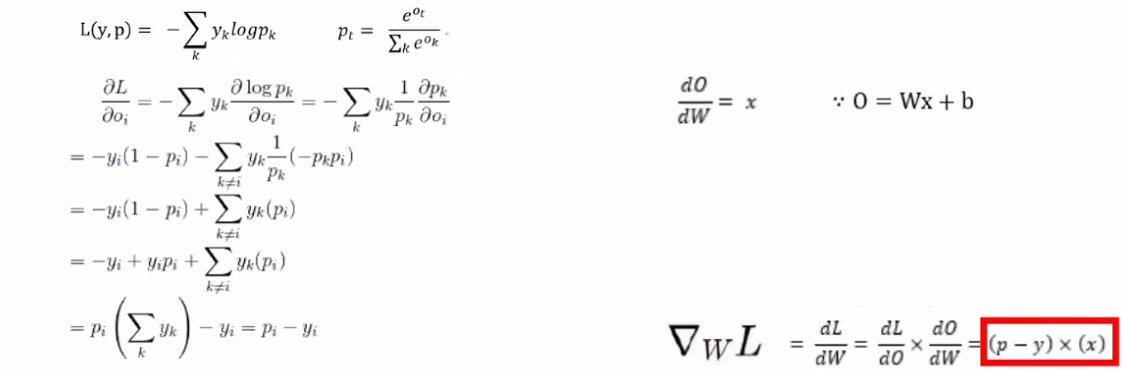
(p-y)*(x) = delta(d) WL = dL/dW(L를 W로 미분한다) W 값에 따라서 Loss가 결정된다.
dy/dx → y를 x로 미분한다. x 변화량에 따른 y 변화량
loss 가 크면 Weight를 크게 수정해야 하고, loss가 0에 가까우면 Weight 값 보정을 작게 해야 한다.
Loss 값에 대한 Weight 값의 책임론을 정량화 시켜 놓은 공식
⇒ 편미분 진행 (Backpropagation)
결과 값과 loss 값이 나오고 후퇴(backward) 후 다시 weight 보정된 값으로 forward 반복하여 loss를 낮추는 게 최종 목표
고양이 이미지의 픽셀값에 중요도를 곱하고 bias를 더해서 출력 결과 나옴
(변수가 하나인 경우)
Image → y1 (W1 * x1 + b1) → y2 (W2 * y1 + b2) ⇒ output을 softmax 적용하여 보정
(W2 (W1*x1+b1)+b2)
사실 학습의 주체는 Weight와 Bias이지만 Weight의 비중이 훨씬 커서 weight 보정하는 데에 치중한다.
0.3 Loss가 나온 것에 대한 W1, b1, W2, b2가 얼마나 영향을 미쳤는지 계산 ⇒ 보정
- Stochastic Gradient Descent (SGD)
- 기본적인 learning-rate의 default가 0.1

- Optimization의 종류
- sgd : 느리지만 평지에 가장 가까움
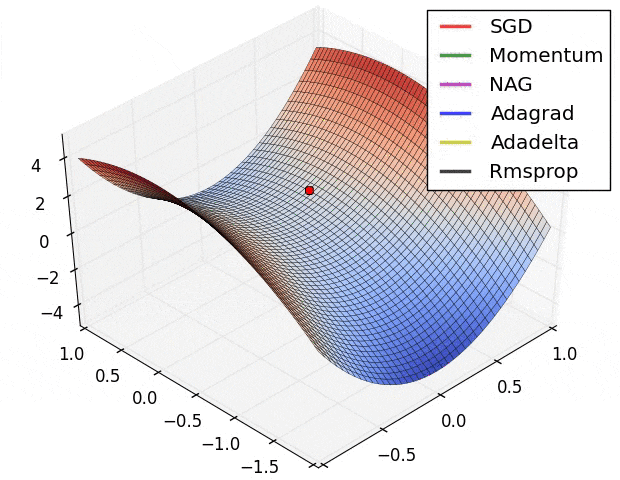

epoch가 증가함에 따라 decay를 감소 시켜야 한다.
초반부엔 Adam과 같이 빨리 내려오는 것, 평지 근처에 왔을 때는 안정적인 SDG 사용하는 게 좋을 수 있음, epoch가 진행됨에 따라 섞어 쓰는 것도 좋음
ex) 5만 개의 train 문제집,1만 개의 모의고사 ⇒ 변형된 문제집 5만 번, 변형된 모의고사 1만 번
변형 darkness, rotation, crop 등
보통 epoch은 train과 validation을 합쳐서 몇 번 학습했는지에 대한 학습 횟수
- Backpropagation

Neural Network에서 input data 8개, output data 4개(클래스 개수)
input data의 출력이 hidden layer1의 입력으로..
hidden layer1의 출력이 hidden layer2의 입력으로..
중간 출력값들을 가지고 출력해보면 첫 고양이 이미지가 못 알아볼 정도의 중간정도 과정을 보여주는데 이것을 feature map 이라고 한다.
⭐ NeuralNet에서 Hyperparameter
hidden layer의 동그라미들을 노드라고 하고, unit 수라고 한다.
input data의 개수 8개, 첫 hidden layer1의 노드 9개이기 때문에 둘 사이의 weight 개수는 8*9 = 72개이다.
모든 layer가 촘촘히 연결되었다는 의미에서 Fully-connected Network이라고 한다.
각각 output 4개의 loss 값을 구해서 전체 Loss를 구했던 0.7이면 에러율이 높다는 것이므로 이전 Weight 값들을 모두 보정하는 과정이 필요하다.
'AI > 딥러닝' 카테고리의 다른 글
| [딥러닝] Neural Network (0) | 2022.04.26 |
|---|---|
| [딥러닝] Optimization Colab 환경 실습 (0) | 2022.04.24 |
| [딥러닝] Computer vision, Classification, Linear Classifier, Loss Function (0) | 2022.04.24 |



댓글