경사하강법 (Gradient Descent)
딥러닝의 가장 기본이 되는 알고리즘
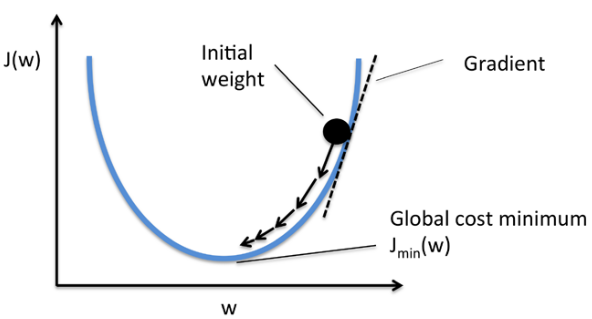
기본 개념은 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복시키는 것입니다.
비용 함수 (Cost Function 혹은 Loss Function)를 최소화하기 위해 반복해서 파라미터를 업데이트 해 나가는 방식입니다.
오차(Error) 정의
Loss Function 혹은 Cost Function을 정의 합니다.
Loss (Cost) Function은 예측값인 y_hat과 y의 차이에 제곱으로 정의합니다.
제곱은 오차에 대한 음수 값을 허용하지 않으며, 이는 Mean Squared Error(MSE)인 평균 제곱 오차 평가 지표와 관련 있습니다.
# MSE 함수를 그대로 파이썬 코드로 옮겨보자
error = ((y_hat - y)**2).mean()
error # 0.380019884330235
학습률 (Learning Rate)

한 번 학습할 때 얼마만큼 가중치(weight)를 업데이트 해야 하는지 학습 양을 의미합니다.
너무 큰 학습률 (Learning Rate)은 가중치 갱신이 크게 되어 자칫 Error가 수렴하지 못하고 발산할 수 있으며,너무 작은 학습률은 가중치 갱신이 작게 되어 가중치 갱신이 충분히 되지 않고, 학습이 끝나 버릴 수 있습니다. 즉 과소 적합되어 있는 상태로 남아 있을 수 있습니다.
오차를 줄이는 방법
- 경사를 타고 내려오면서 오차를 줄여 나가는 방법
- 오차가 최소가 될 수 있도록 W와 bias 값을 보정하는 방법

loss가 최소가 되는 최적의 기울기를 찾자 ⇒ 가장 경사가 큰 기울기를 찾아 내려오면 된다.
그래프의 기울기(W값)가 평탄해질 때까지 반복하면서 고도가 크다면 보정을 더 크게 진행하자.
만약 loss가 작다 ⇒ 보정을 작게 해야 한다
loss가 크다 ⇒ 값의 update가 많이 되어야 한다, 보정을 크게 해야 한다

Linear Regression을 활용하여 섭씨온도(C, Celsius)를 화씨온도(F, Fahrenheit)로 변환해주는 공식을 만들수 있다.
섭씨온도과 화씨온도의 관계는 앞에서 우리가 살펴보았던 선형회귀의 관계를 가지고 있다.
H(x) = aX + b 에서처럼, F = C*1.8 +32
이때, 1.8과 32라는 값을 모르고 있다고 가정하고, 머신러닝 알고리즘을 이용해서 주어진 섭씨 온도와 화씨온도 데이타 만으로 이 값들을 찾아내는 실습을 진행해보도록 하겠다.
Generate Dataset
선형회귀 문제를 다루기 위한 학습용 데이타셋을 생성
0도에서 100도 사이의 값을 갖는 섭씨온도 데이타를 100개 만들어보자 이 데이타가 해당 머신러닝 알고리즘에서 사실상 Feature가 될 것이다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 섭씨 온도
C=np.random.randint(0,100, size=100)
C
C=np.random.randint(low=0,high=100, size=100)
C
'''
array([87, 30, 9, 83, 10, 11, 85, 84, 39, 81, 48, 58, 83, 73, 83, 15, 68,
8, 3, 73, 59, 58, 47, 82, 77, 38, 53, 76, 18, 86, 27, 11, 57, 70,
13, 61, 21, 93, 90, 77, 7, 45, 37, 85, 83, 62, 35, 34, 16, 49, 78,
57, 86, 28, 63, 56, 74, 12, 1, 36, 1, 16, 73, 59, 92, 85, 50, 94,
26, 70, 29, 47, 42, 40, 38, 73, 32, 43, 86, 9, 69, 68, 98, 1, 80,
28, 66, 73, 26, 50, 72, 92, 47, 79, 8, 39, 65, 40, 1, 6])
'''
print(C.shape) # (100,)
print(C[:10]) # [87 30 9 83 10 11 85 84 39 81]
섭씨온도 데이터에 상응하는 화씨온도를 생성
알고 있던 기존의 섭씨-화씨변환 공식을 적용해서 위 섭씨온도 데이터에 대응하는 화씨온도 데이타를 생성.
이 데이터가 오늘 다룰 학습 모델 알고리즘의 Label이 될 것이다.
화씨온도 = 섭씨온도 * 1.8 + 32
F = C * 1.8 + 32
F
'''
array([188.6, 86. , 48.2, 181.4, 50. , 51.8, 185. , 183.2, 102.2,
177.8, 118.4, 136.4, 181.4, 163.4, 181.4, 59. , 154.4, 46.4,
37.4, 163.4, 138.2, 136.4, 116.6, 179.6, 170.6, 100.4, 127.4,
168.8, 64.4, 186.8, 80.6, 51.8, 134.6, 158. , 55.4, 141.8,
69.8, 199.4, 194. , 170.6, 44.6, 113. , 98.6, 185. , 181.4,
143.6, 95. , 93.2, 60.8, 120.2, 172.4, 134.6, 186.8, 82.4,
145.4, 132.8, 165.2, 53.6, 33.8, 96.8, 33.8, 60.8, 163.4,
138.2, 197.6, 185. , 122. , 201.2, 78.8, 158. , 84.2, 116.6,
107.6, 104. , 100.4, 163.4, 89.6, 109.4, 186.8, 48.2, 156.2,
154.4, 208.4, 33.8, 176. , 82.4, 150.8, 163.4, 78.8, 122. ,
161.6, 197.6, 116.6, 174.2, 46.4, 102.2, 149. , 104. , 33.8,
42.8])
'''
print(F.shape) # (100,)
print(F[:10]) # [188.6 86. 48.2 181.4 50. 51.8 185. 183.2 102.2 177.8]
Visualize
위에서 우리가 만든 Feature와 Label을 matplot을 이용해서 시각화
plt.scatter(C, F)
plt.xlabel('Celsius Temperature')
plt.ylabel('Fahrenheit Temperature')
plt.show()

Bias (편향 찾기)
Weight는 1.8로 주고 Bias를 보정하면서 직관적인 방법으로 한번 찾아보자.
bias를 안 주고 32를 찾을 건데 이때 내가 어떤 원리(기법)로 bias를 찾는지 미분, 기울기 값을 찾아낸다. 사실 편미분 원리이다.
X = C
y = F
w = 1.8
# 최소값 -1.0
b = np.random.uniform(low=-1.0, high=+1.0) # 학습 가능한 범위의 값을 지정
w,b # (1.8, -0.7994145485504731)
y_predict = w * X + b
y_predict[:10]
'''
array([155.80058545, 53.20058545, 15.40058545, 148.60058545,
17.20058545, 19.00058545, 152.20058545, 150.40058545,
69.40058545, 145.00058545])
'''
plt.scatter(C, F)
plt.plot(C, y_predict, c='r')
plt.xlabel('Celsius Temperature')
plt.ylabel('Fahrenheit Temperature')
plt.show()

위의 두 그래프는 기울기는 똑같고 오차만큼 편향을 빼면 원래 기울기를 찾을 수 있다.
loss에 따라서 W값을 보정해 나간다. 즉, 원래 bias에서 오차만큼 빼서 bias를 갱신해준다.
여기서 기울기는 똑같고 y 절편만 다르기 때문에 오차는 실제 y 값과 예측한 y값의 차이와 같다.
b = b-(y_predict-y).mean()
b # 32.000000000000014
y_predict = w * X + b
y_predict[:10] # array([188.6, 86. , 48.2, 181.4, 50. , 51.8, 185. , 183.2, 102.2,
177.8])
plt.scatter(C, F)
plt.plot(C, y_predict, c='r')
plt.xlabel('Celsius Temperature')
plt.ylabel('Fahrenheit Temperature')
plt.show()

정규분포에 해당하는 w,b값을 랜덤하게 지정해서 초기화
실제 값과 예측치 결과 값과의 차이를 시각화 해서 확인
w = np.random.uniform(low=-1.0, high= 1.0) # W 값 랜덤
b = np.random.uniform(low=-1.0, high= 1.0) # bias 값 랜덤
w,b # (-0.5160114794318065, 0.3413652741080968)
y_predict = w * X + b
y_predict[0:10] # 예측값 구하기
'''
array([-44.55163344, -15.13897911, -4.30273804, -42.48758752,
-4.81874952, -5.334761 , -43.51961048, -43.003599 ,
-19.78308242, -41.45556456])
'''
plt.scatter(C, F)
plt.plot(C, y_predict, 'r')

Gradient Descent
가중치(Weight, W), 편향(Bias, B) 찾기
이제 경사하강법(Gradient Descent)을 사용하여 섭씨온도를 화씨온도로 변환해줄 주 있는 공식을 찾아보겠다.
공식의 세부내용은 모른다치고, 두 변수(X,y)가 선형(Linear)과 관계있음을 가정(y=X * w + b)하여 가중치(weight)와 편차(bias)를 정의해 둔다.
그리고 경사하강법을 이용해서 선형회귀를 학습시킨다.
학습이 완료되면, 얻어진 최적의 가중치와 편차로 섭씨온도를 화씨온도로 변환해주는 공식을 만들어 줄 수 있다.
학습은 모든 epoch이 끝날 때까지 반복할 수도 있지만, 여기선 오차(error)가 0.1 이하가 되면 break 키워드를 사용해서 학습을 종료한다.
Gradient Descent에서는 learning rate를 꼭 곱해줘야 한다.
num_epoch = 100000 # 학습 횟수 보통 epcch 횟수는 100번으로 지정함
learning_rate = 0.0003
w = np.random.uniform(low=-1.0, high=1.0)
b = np.random.uniform(low=-1.0, high=1.0)
for epoch in range(num_epoch):
y_predict = w * X + b # 처음 학습할 때 예측값 뽑아내기
# 얼마나 예측을 잘 했는지 error(오차) 구하기, 오차에 **제곱**? 절댓값?
error = np.abs(y_predict-y).mean() # min absolute error
# if error<0.001: # 에러율 더 낮아짐!
if error<0.1: # 평지에 거의 가까워 질 때! 평지 == cost가 0
break
# 값을 보정한다.. Weight, bias 값을 보정하자
w = w-learning_rate*((y_predict-y) * X).mean()
b = b-learning_rate*(y_predict-y).mean() # Gradientdescent에서 가장 중요한 점! learning rate를 곱해줘야 한다!
if epoch % 10000 == 0:
print(f"{epoch:5} w = {w:.6f}, b = {b:.3f}, error = {error:.3f}")
print("---------" * 10)
print(f"{epoch:5} w = {w:.3f}, b = {b:.3f}, error = {error:.3f}")
'''
0 w = 2.350384, b = -0.241, error = 169.869
10000 w = 2.038905, b = 16.068, error = 6.261
20000 w = 1.918056, b = 24.127, error = 3.094
30000 w = 1.858338, b = 28.109, error = 1.529
40000 w = 1.828828, b = 30.077, error = 0.756
50000 w = 1.814246, b = 31.050, error = 0.373
60000 w = 1.807040, b = 31.531, error = 0.184
----------------------------------------------
68689 w = 1.804, b = 31.746, error = 0.100
'''
loss(error) 값을 보고 고도를 낮출 수 있는 (0에 가깝게 할 수 있는 최적의 W와 bias)값을 찾아내는 경사하강법!
Predict

선형 회귀의 학습이 끝났으면, 이제 이 머신러닝 알고리즘을 활용하여 변환공식을 완성하고, 주어진 섭씨온도를 화씨온도로 변환(혹은 섭씨온도로 화씨온도를 예측)할 수 있다.
앞서 만들어준 데이터를 그대로 활용하여 주어진 섭씨온도(C)로 화씨온도를 예측해보자.
y_predict = w * C + b
y_predict[0:5]
# array([189.51881399, 84.34025966, 45.59026596, 182.13786281, 47.43550375])
result = pd.DataFrame({"C": C, "F": F, "F(predict)": y_predict})
print(result.shape)
result.head(10)

Visualize
결과가 잘 나왔으면, 예측한 값과 실제값을 비교하여 시각화를 통해 잘 예측이 되었는지 확인
plt.scatter(C, F)
plt.plot(C, y_predict, 'r')
'AI > 머신러닝' 카테고리의 다른 글
| [머신러닝] 회귀 모델 (Regression Models) 1 (0) | 2022.04.16 |
|---|---|
| [머신러닝] 경사하강법 (Gradient Descent) 2 (0) | 2022.04.16 |
| [머신러닝] 최소제곱법을 활용한 LinearRegression (0) | 2022.04.12 |
| [머신러닝] 데이터 전처리 | 표준화, 정규화 (0) | 2022.04.12 |
| [머신러닝] K-최근접 이웃(K-NN) 분류 알고리즘 - 실습 (0) | 2022.04.11 |




댓글