회귀 모델 (Regression Models)
모델별 성능 확인을 위한 함수
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.metrics import mean_squared_error
from IPython.display import Image
np.set_printoptions(suppress=True, precision=3)
my_predictions = {}
my_pred = None
my_actual = None
my_name = None
colors = ['r', 'c', 'm', 'y', 'k', 'khaki', 'teal', 'orchid', 'sandybrown',
'greenyellow', 'dodgerblue', 'deepskyblue', 'rosybrown', 'firebrick',
'deeppink', 'crimson', 'salmon', 'darkred', 'olivedrab', 'olive',
'forestgreen', 'royalblue', 'indigo', 'navy', 'mediumpurple', 'chocolate',
'gold', 'darkorange', 'seagreen', 'turquoise', 'steelblue', 'slategray',
'peru', 'midnightblue', 'slateblue', 'dimgray', 'cadetblue', 'tomato'
]
def plot_predictions(name_, pred, actual):
df = pd.DataFrame({'prediction': pred, 'actual': y_test})
df = df.sort_values(by='actual').reset_index(drop=True)
plt.figure(figsize=(11, 8))
plt.scatter(df.index, df['prediction'], marker='x', color='r')
plt.scatter(df.index, df['actual'], alpha=0.7, marker='o', color='black')
plt.title(name_, fontsize=15)
plt.legend(['prediction', 'actual'], fontsize=12)
plt.show()
def mse_eval(name_, pred, actual):
global my_predictions, colors, my_pred, my_actual, my_name
my_name = name_
my_pred = pred
my_actual = actual
plot_predictions(name_, pred, actual)
mse = mean_squared_error(pred, actual)
my_predictions[name_] = mse
y_value = sorted(my_predictions.items(), key=lambda x: x[1], reverse=True)
df = pd.DataFrame(y_value, columns=['model', 'mse'])
print(df)
min_ = df['mse'].min() - 10
max_ = df['mse'].max() + 10
length = len(df) / 2
plt.figure(figsize=(9, length))
ax = plt.subplot()
ax.set_yticks(np.arange(len(df)))
ax.set_yticklabels(df['model'], fontsize=12)
bars = ax.barh(np.arange(len(df)), df['mse'], height=0.3)
for i, v in enumerate(df['mse']):
idx = np.random.choice(len(colors))
bars[i].set_color(colors[idx])
ax.text(v + 2, i, str(round(v, 3)), color='k', fontsize=12, fontweight='bold', verticalalignment='center')
plt.title('MSE Error', fontsize=16)
plt.xlim(min_, max_)
plt.show()
def add_model(name_, pred, actual):
global my_predictions, my_pred, my_actual, my_name
my_name = name_
my_pred = pred
my_actual = actual
mse = mean_squared_error(pred, actual)
my_predictions[name_] = mse
def remove_model(name_):
global my_predictions
try:
del my_predictions[name_]
except KeyError:
return False
return True
def plot_all():
global my_predictions, my_pred, my_actual, my_name
plot_predictions(my_name, my_pred, my_actual)
y_value = sorted(my_predictions.items(), key=lambda x: x[1], reverse=True)
df = pd.DataFrame(y_value, columns=['model', 'mse'])
print(df)
min_ = df['mse'].min() - 10
max_ = df['mse'].max() + 10
length = len(df) / 2
plt.figure(figsize=(9, length))
ax = plt.subplot()
ax.set_yticks(np.arange(len(df)))
ax.set_yticklabels(df['model'], fontsize=12)
bars = ax.barh(np.arange(len(df)), df['mse'], height=0.3)
for i, v in enumerate(df['mse']):
idx = np.random.choice(len(colors))
bars[i].set_color(colors[idx])
ax.text(v + 2, i, str(round(v, 3)), color='k', fontsize=12, fontweight='bold', verticalalignment='center')
plt.title('MSE Error', fontsize=16)
plt.xlim(min_, max_)
plt.show()
✅ 보스턴 집 값 데이터
컬럼 소개
속성 수 : 13
- CRIM: 범죄율
- ZN: 25,000 평방 피트 당 주거용 토지의 비율
- INDUS: 비소매(non-retail) 비즈니스 면적 비율
- CHAS: 찰스 강 더미 변수 (통로가 하천을 향하면 1; 그렇지 않으면 0)
- NOX: 산화 질소 농도 (천만 분의 1)
- RM:주거 당 평균 객실 수
- AGE: 1940 년 이전에 건축된 자가 소유 점유 비율
- DIS: 5 개의 보스턴 고용 센터까지의 가중 거리
- RAD: 고속도로 접근성 지수
- TAX: 10,000 달러 당 전체 가치 재산 세율
- PTRATIO 도시 별 학생-교사 비율
- B: 1000 (Bk-0.63) ^ 2 여기서 Bk는 도시 별 검정 비율입니다.
- LSTAT: 인구의 낮은 지위
- target: 자가 주택의 중앙값 (1,000 달러 단위)
데이터 로드 (load_boston)
data['data']에는 X 데이터, data['feature_names']에는 컬럼 명입니다.
import pandas as pd
from sklearn.datasets import load_boston
data = load_boston()
# data['data']에는 X 데이터, data['feature_names']에는 컬럼 명입니다.
# key 값을 이용해서 feature와 label 추출
df = pd.DataFrame(data['data'], columns=data['feature_names'])
df.head()

target 데이터도 Column 에 추가합니다.

학습(train) / 테스트(test) 용 데이터를 분할 합니다.
train_test_split()의 데이터 분할 dafault는 75:25 로 나뉩니다.
또한, shuffle 기능도 default이기 때문에 데이터를 무작위로 나눌 수 있습니다.
from sklearn.model_selection import train_test_split
SEED=30
x_train, x_test, y_train, y_test = train_test_split(df.drop('target', axis=1), df['target'],random_state=SEED)
x_train.shape, x_test.shape # ((379, 13), (127, 13))
x_train.head()
아래 출력된 Dataframe을 보시면 인덱스 번호가 무작위로 섞여있는 것을 볼 수 있습니다.

LinearRegression
mse_eval('LinearRegression', pred, y_test)

LinearRegressor 모델 만들기
• n_jobs: CPU코어의 사용
from sklearn.linear_model import LinearRegression
model = LinearRegression(n_jobs=-1)
# 학습
model.fit(x_train, y_train)
# 예측
pred = model.predict(x_test) # 테스트용 데이터로 에측 데이터 뽑기
mse_eval('LinearRegression', pred, y_test) # 예측 결과와 실제 데이터가 같은지 비교
# mse_eval(name_, pred, actual)
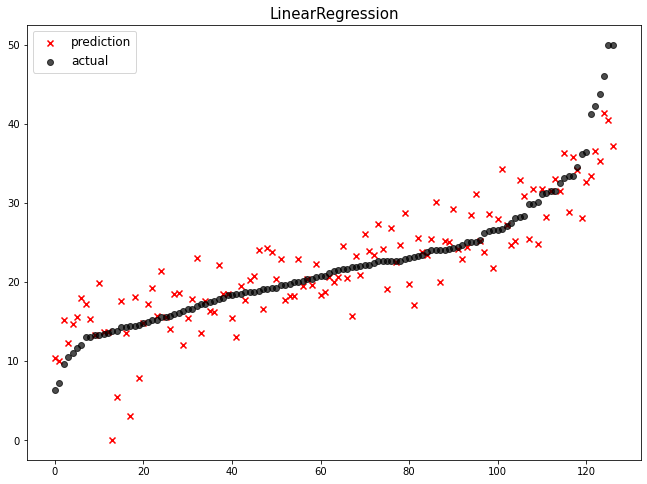
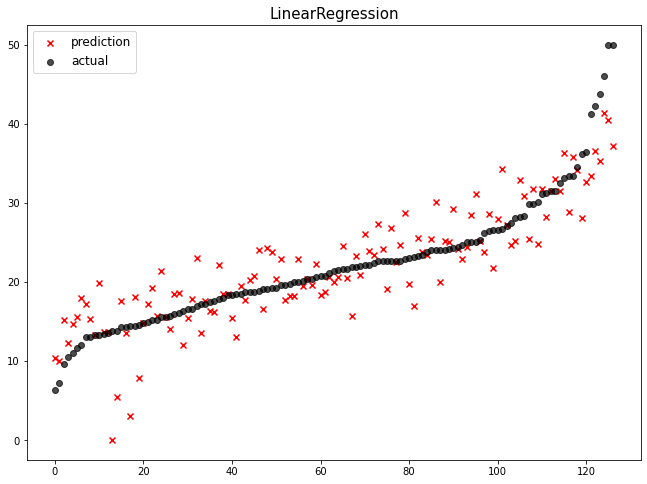
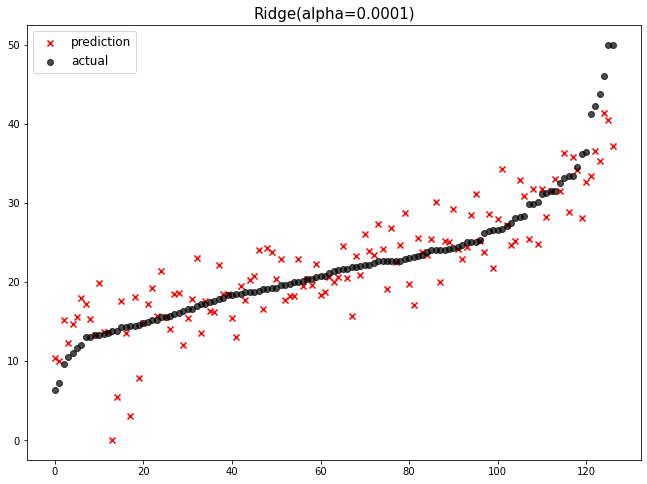
까만 점들이 주택 가격, 주택가격이 낮은 것부터 높은 것까지 정렬
빨간 x 표시가 예측값
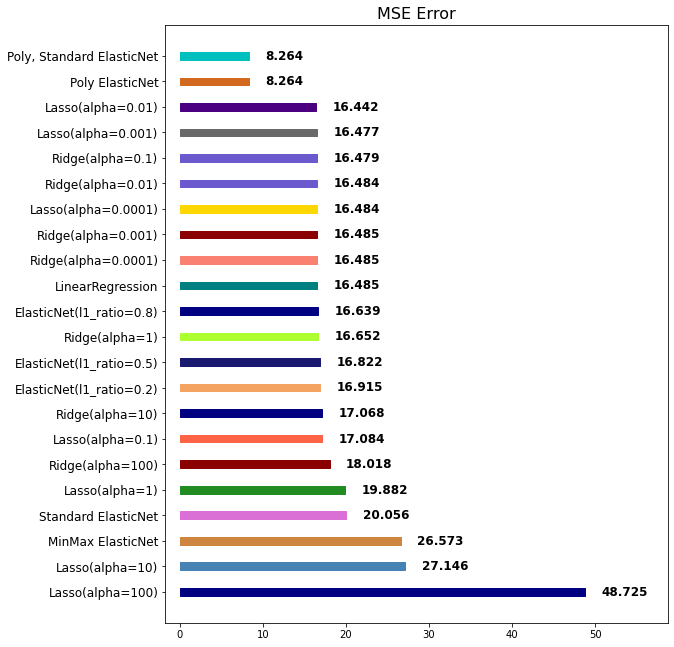
LinearRegression의 error율은 16.485로 더 줄여 10% 이내로 향상 시키는 것을 목표로 잡아야 합니다.
오차가 크게 나온 이유
- 주택가격이 높은 부분은 예측하지 못 함
- 주택가격이 낮은 부분의 예측값 과 실제 값의 오차가 큼
위의 결과로 전체 예측률에 패널티로 크게 작용하여 성능이 낮아진 것입니다.
이상치 값들의 원인으로는 라벨과 선형적인 관계가 아닐 확률이 있습니다.
따라서 이 오차를 줄이기 위해서는 이상치 값과 칼럼과의 선형적 관계를 이루고 있지 않는 것을 찾아내어 차수(다항식)를 높여서 곡선 그래프로 만들어서 개선 가능합니다.
다중회귀, 다항회귀
y = W1x1 + W2x2 + W3*x3 + ... + b머신러닝에서 학습의 주체가 W와 b입니다.
학습을 한다는 것을 패턴을 찾는 것이고, 패턴을 찾는다는 것은 예를 들어 ‘방의 개수’ 칼럼이 주택 가격을 예측하는 데에 비중이 얼마인지 알아내는 것입니다.
따라서 칼럼마다 중요하게 생각되는 칼럼의 가중치는 크게, 그렇지 않은 칼럼에는 가중치를 낮게 줍니다.
결국 그래프의 형태는 칼럼마다 가중치의 variance가 커서, 다양해서 규제를 해줘야 합니다.
그래프에서 가중치의 격차가 큰 것들을 조금씩 깎아내어(가중치가 높은 것은 줄이고, 가중치가 낮은 것은 높이기) 진폭을 낮춰줘야 합니다.
따라서 규제(Regularization) 과정을 거치면 그래프의 격차가 완만해질 수 있습니다.
가중치 값의 간극이 너무 크게 되면 Overffing될 확률이 높아지기 때문에 epoch 단계마다 규제가 필요합니다.
⇒ Overfitting과 성능은 서로 trade off 관계(반비례)이기 때문에 데이터 가중치의 다양성을 줄이기 위해서는 규제가 필수적입니다.
이때 규제는 특정 칼럼에만 적용되는 것이 아니라 전체 컬럼에 대해 적용되어 전반적인 규제가 이루어집니다.
규제를 통해 얻고자 하는 결과는 W 값이 한 쪽으로 과도하게 몰리는 것을 방지하는 것입니다.
규제를 적용한 선형 회귀 모델 중 최소제곱법으로 예측 선을 알아내는 것 ⇒ LinearRegression
경사하강법으로 예측선 알아내는 것 ⇒ SGDRegression
위 두 모델 중 LinearRegression에 규제를 적용시켜 새로운 모델을 만들어낼 수 있습니다.
LinearRegression에 L1 규제, L2 규제를 적용시킬 수 있습니다.
이 모델을 규제 선형 회귀 모델이라고 합니다.
규제 (Regularization)
학습이 과대적합 되는 것을 방지하고자 일종의 penalty를 부여하는 것
L2 규제 (L2 Regularization)
- 각 가중치 제곱의 합에 규제 강도(Regularization Strength) λ를 곱한다.
- λ를 크게 하면 가중치가 더 많이 감소되고(규제를 중요시함), λ를 작게 하면 가중치가 증가한다(규제를 중요시하지 않음).
L1 규제 (L1 Regularization)
- 가중치의 제곱의 합이 아닌 가중치의 절대값을 더한 값에 규제 강도(Regularization Strength) λ를 곱하여 오차에 더한다.
- 어떤 가중치(w)는 실제로 0이 된다. 즉, 모델에서 완전히 제외되는 특성이 생기는 것이다.
L2 규제가 L1 규제에 비해 더 안정적이라 일반적으로는 L2규제가 더 많이 사용된다.
규제 강도(Alpha)
- 모델을 단순하게 해주고 학습 데이터 성능과 평가 데이터 성능 사이를 절충할 방법
- 과대적합이 발생한 상황에서 모델의 alpha 값을 증가시키면 학습 성능은 감소하지만 평가 성능은 증가함
- Alpha의 값이 너무 크게 지정하는 경우 가중치에 대한 규제가 강해지며 너무 모델이 단순하여 과소적합 현상이 발생할 수 있음
- Alpha의 값이 아주 작게 하거나 0으로 지정하는 경우 가중치에 대한 규제가 약해지며 과대적합 현상이 발생할 수 있음 (alpha의 값이 0인 경우 Linear Regression과 동일함)
1. Ridge (L2 Regularization)
- L2 규제 계수를 적용합니다.
- 선형회귀에 가중치 (weight)들의 제곱합에 대한 최소화를 추가합니다.
주요 hyperparameter
- alpha : 규제 계수
수식
𝐸𝑟𝑟𝑜𝑟=𝑀𝑆𝐸+α𝑤2
규제 전 LinearRegression
from sklearn.linear_model import LinearRegression
model = LinearRegression(n_jobs=-1)
model.fit(x_train, y_train) # LinearRegression(n_jobs=-1) 학습
# 예측
pred = model.predict(x_test)
mse_eval('LinearRegression', pred, y_test)
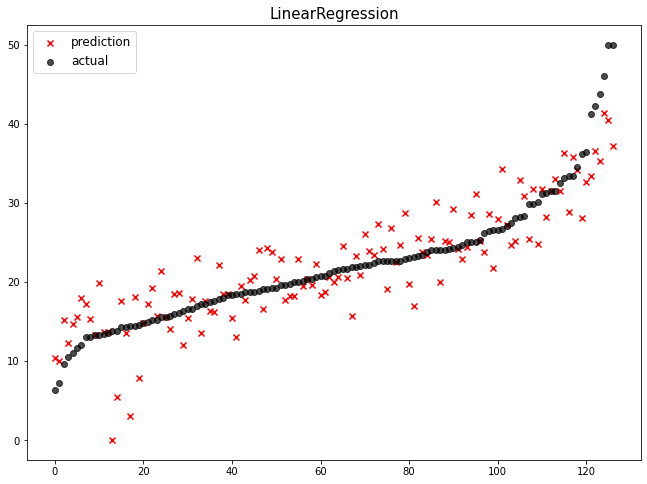

규제 계수(alpha)를 정의합니다.
from sklearn.linear_model import Ridge
alphas = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001]
for alpha in alphas:
ridge = Ridge(alpha=alpha) # Ridge 모델 생성
ridge.fit(x_train, y_train) # 학습
pred = ridge.predict(x_test) # 예측
add_model('Ridge(alpha={})'.format(alpha), pred, y_test)
plot_all()
# 0.1 규제 강도를 줘야 하는 군!
# 규제 강도가 작을 수록 0에 가깝다
# 규제를 크게 줘서 overfitting은 줄일 수 있지만 학습량이 부족하다..?
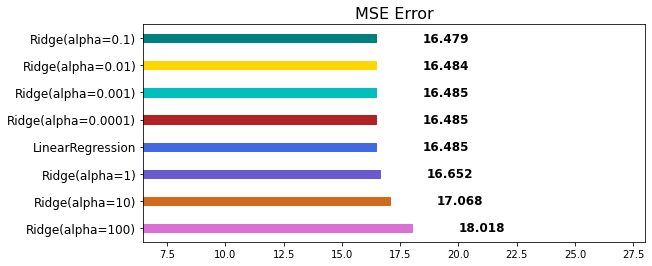
규제 강도를 0.1(alpha=0.1) 정도 줘야 예측률이 높다는 것을 알 수 있습니다.
또한, 규제 강도가 작을 수록 LinearRegression(규제를 적용하지 않은 선형 회귀 모델)과 별 다를 게 없다는 것을 알 수 있습니다.
반대로 규제 강도를 너무 크게 주면 Overfitting은 피할 수 있지만 학습량이 적어서 성능이 오히려 떨어졌습니다.
coef_는 feature의 가중치를 보여줍니다.
학습이 끝난다는 의미는 각 칼럼별 적용된 가중치(중요도)에 대해 출력해볼 수 있습니다.
가중치(weight)를 토대로 회귀 예측시 어떤 feature가 주요하게 영향을 미쳤는지 보여 줍니다.
# 현재 가지고 있는 칼럼들 출력
x_train.columns
'''
Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
'PTRATIO', 'B', 'LSTAT'],
dtype='object')
'''
가중치 값에서 음/양수를 따지지 말고 숫자의 크고 작음에 집중해야 합니다.
독보적으로 수치가 큰 -18.012는 아파트 가격에 대해 영향력이 가장 크다고 할 수 있습니다.
-18.012 수치에 해당하는 칼럼은 NOX(산화질소량)이고 해당 칼럼이 반비례 관계(음수이기 때문)로 아파트 가격에 가장 중요한 영향을 끼치는 것으로 볼 수 있습니다.
다음으로 두 번째로 아파트 가격에 대해 영향력이 큰 것은 3.729 수치를 보이는 RM 방의 개수입니다.
ridge.coef_ # 칼럼별 가중치
# - 와 + 는 반비례, 비례 관계
'''
array([ -0.115, 0.04 , -0.003, 3.487, -18.012, 3.729, 0.005,
-1.529, 0.325, -0.013, -0.957, 0.006, -0.557])
'''
DataFrame으로 feature별 가중치를 시각화 합니다.
zip() 함수로 칼럼별 가중치를 짝지어 출력합니다.
list(zip(x_train.columns, ridge.coef_)) # zip으로 묶고 list로 변환해야 함
'''
[('CRIM', -0.11473573559118938),
('ZN', 0.04045244824086786),
('INDUS', -0.0028785170940756953),
('CHAS', 3.486691649056479),
('NOX', -18.012494293774203),
('RM', 3.7289172052704527),
('AGE', 0.004546036313653151),
('DIS', -1.5293992458368861),
('RAD', 0.32479345169343016),
('TAX', -0.013133583308927818),
('PTRATIO', -0.9572456861802442),
('B', 0.006368762657410718),
('LSTAT', -0.5573495745859701)]
'''
보기 쉽게 데이터프레임으로 시각화 해봅니다.
각 칼럼별 가중치는 음/양수 상관 없이 수치의 크기만 보기 위해 절댓값을 적용해줍니다.
fi = pd.DataFrame(list(zip(x_train.columns, abs(ridge.coef_))))
fi.columns = ['features', 'importances']
# 아파트 가격에 영향력 높은 순으로 정렬
fi.sort_values(by='importances', ascending=False)
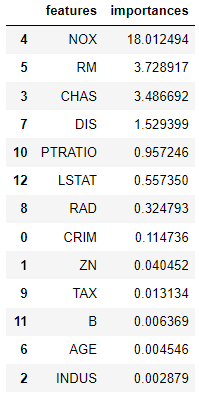
학습 완료 후 모델의 가중치 찍어보기
def plot_coef(columns, coef):
# 데이터 프레임 만드는 코드
coef_df = pd.DataFrame(list(zip(columns, coef)))
coef_df.columns=['feature', 'coef']
coef_df = coef_df.sort_values('coef', ascending=False).reset_index(drop=True)
# 시각화 코드
fig, ax = plt.subplots(figsize=(9, 7))
ax.barh(np.arange(len(coef_df)), coef_df['coef'])
idx = np.arange(len(coef_df))
ax.set_yticks(idx)
ax.set_yticklabels(coef_df['feature'])
fig.tight_layout()
plt.show()
이번에는, alpha(규제강도) 값에 따른 coef 의 차이를 확인해 봅시다
# 규제 강도에 따라 weight 값이 어떻게 달라지는지 확인해보자
ridge_100 = Ridge(alpha=100) # 규제 강도 100
ridge_100.fit(x_train, y_train)
ridge_pred_100 = ridge_100.predict(x_test)
ridge_001 = Ridge(alpha=0.001) # 규제 강도 작게 줌
ridge_001.fit(x_train, y_train)
ridge_pred_001 = ridge_001.predict(x_test)
plot_coef(x_train.columns, ridge_100.coef_)
- Ridge 규제 강도 alpha=100일 때
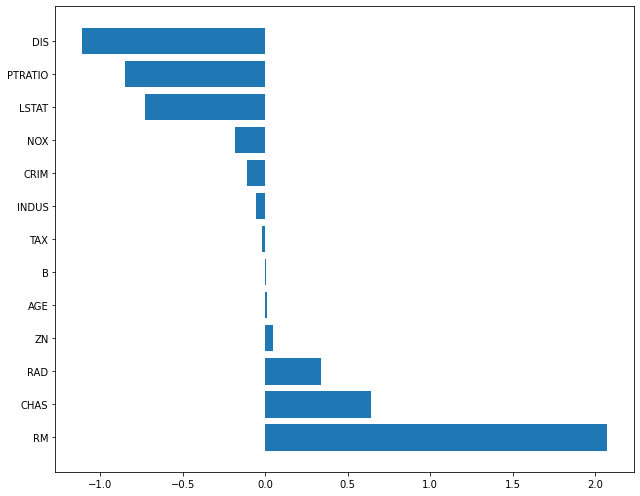
- Ridge 규제 강도 alpha=0.01일 때
plot_coef(x_train.columns, ridge_001.coef_)
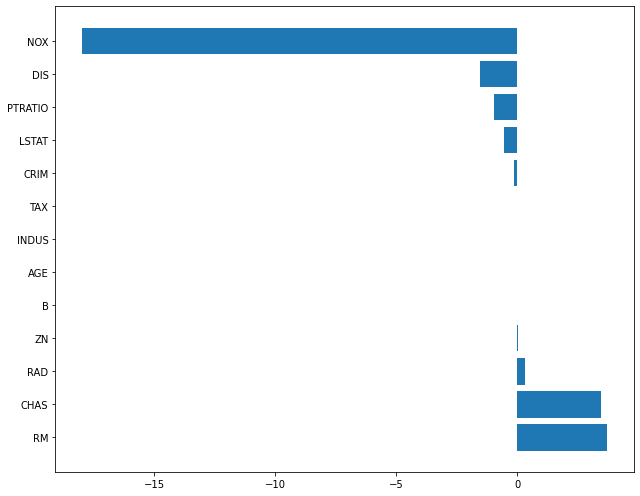
위의 그래프를 통해 규제 강도에 따라서 칼럼의 가중치 weight 값이 달라진다는 것을 알 수 있습니다.
2. Lasso (L1 Regularization)
Lasso(Least Absolute Shrinkage and Selection Operator)
- 선형 회귀에 L1 규제 계수를 적용합니다.
- 가중치(weight)의 절대 값의 합을 최소화 하는 계수를 추가 합니다.
- 불필요한 회귀 계수를 급격히 감소, 0으로 만들어 제거합니다.
- 특성(Feature) 선택에 유리합니다.
주요 hyperparameter
- alpha: L1 규제 계수
수식
𝐸𝑟𝑟𝑜𝑟=𝑀𝑆𝐸+α|𝑤|
from sklearn.linear_model import Lasso
alphas = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001]
for alpha in alphas:
lasso = Lasso(alpha=alpha)
lasso.fit(x_train, y_train)
pred = lasso.predict(x_test)
add_model('Lasso(alpha={})'.format(alpha), pred, y_test)
plot_all()
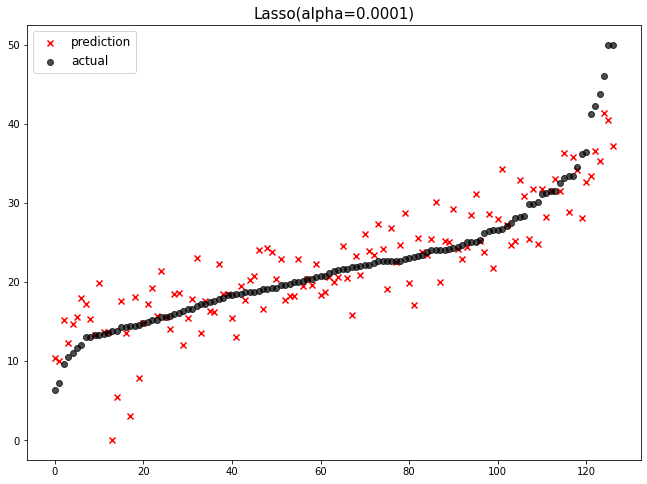
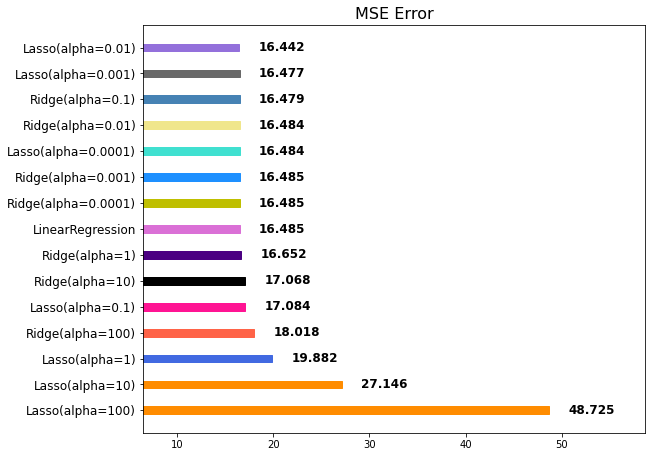
위 그래프를 보면 Lasso가 1위부터 랭크되어 있음을 알 수 있습니다.
하지만 Lasso의 규제 강도가 100이라면 성능이 급격히 안 좋아지고, Ridge와 동일하게 규제 강도가 0에 가까울 수록 아무런 규제를 적용하지 않은 LinearRegression과 비슷한 성능을 보입니다.
여러 개의 모델의 성능을 비교 분석하여 어떤 모델을 선택할 수 있는지 알 수 있습니다.
- 규제 강도 0.01 작을 때
lasso_100 = Lasso(alpha=100)
lasso_100.fit(x_train, y_train)
lasso_pred_100 = lasso_100.predict(x_test)
lasso_001 = Lasso(alpha=0.001)
lasso_001.fit(x_train, y_train)
lasso_pred_001 = lasso_001.predict(x_test)
plot_coef(x_train.columns, lasso_001.coef_)
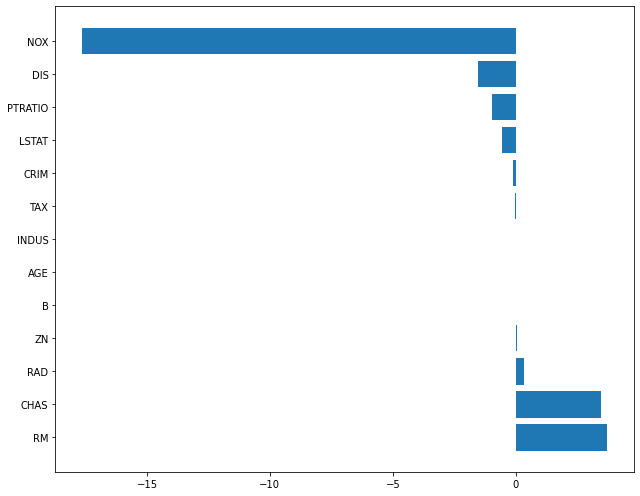
lasso_001.coef_
'''
array([ -0.115, 0.04 , -0.004, 3.468, -17.66 , 3.73 , 0.004,
-1.523, 0.324, -0.013, -0.954, 0.006, -0.558])
'''
- 규제 강도 100으로 클 때
Lasso 모델에 너무 큰 alpha 계수를 적용하면 대부분의 feature들의 가중치가 0으로 수렴 합니다. 강도에 따른 극단적인 결과를 보이는 것이 Lassso의 치명적인 단점입니다.
plot_coef(x_train.columns, lasso_100.coef_)

'AI > 머신러닝' 카테고리의 다른 글
| [머신러닝] 로지스틱 (0) | 2022.04.16 |
|---|---|
| [머신러닝] 회귀 모델 (Regression Models) 2 (0) | 2022.04.16 |
| [머신러닝] 경사하강법 (Gradient Descent) 2 (0) | 2022.04.16 |
| [머신러닝] 경사하강법 (Gradient Descent) 1 (0) | 2022.04.16 |
| [머신러닝] 최소제곱법을 활용한 LinearRegression (0) | 2022.04.12 |




댓글