ElasticNet
Elastic Net 회귀모형은 가중치의 절대값의 합(L1)과 제곱합(L2)을 동시에 제약 조건으로 가지는 모형입니다.
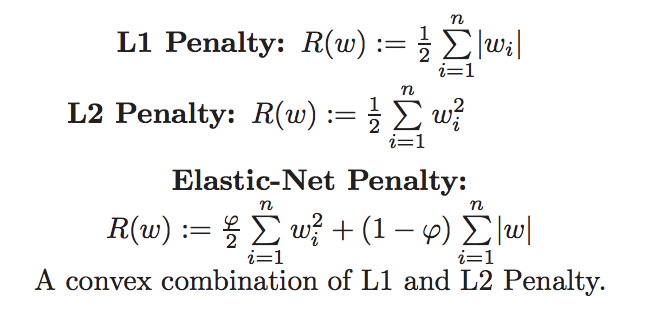
주요 hyperparameter
alpha: 규제 계수
l1_ratio (default=0.5)
- l1_ratio = 0 (L2 규제만 사용).
- l1_ratio = 1 (L1 규제만 사용).
- 0 < l1_ratio < 1 (L1 and L2 규제의 혼합사용)
ElasticNet 속성에 l1_ratio에 0.2를 주면 L1 규제 20%, L2 규제 80% 적용한다는 의미이고,
l1_ratio에 0.8를 주면 L1 규제 80%, L2 규제 20% 적용한다는 의미입니다.
from sklearn.linear_model import ElasticNet
alpha = 0.01 # alpha 값은 고정
ratios = [0.2, 0.5, 0.8]
for ratio in ratios:
elasticnet = ElasticNet(alpha=alpha, l1_ratio=ratio)
elasticnet.fit(x_train, y_train)
pred = elasticnet.predict(x_test)
add_model('ElasticNet(l1_ratio={})'.format(ratio), pred, y_test)
plot_all()
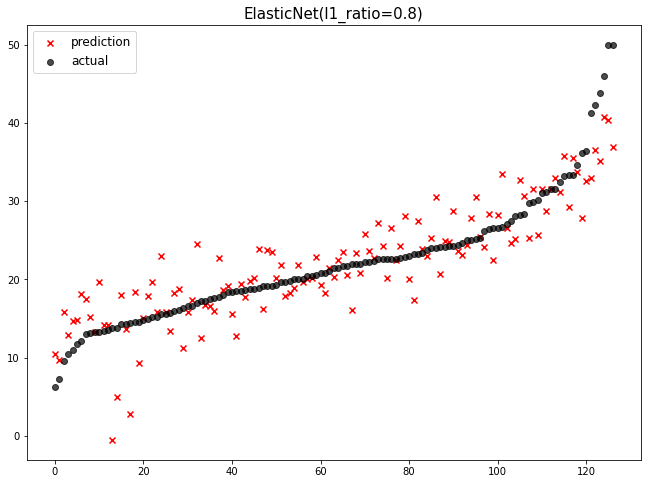
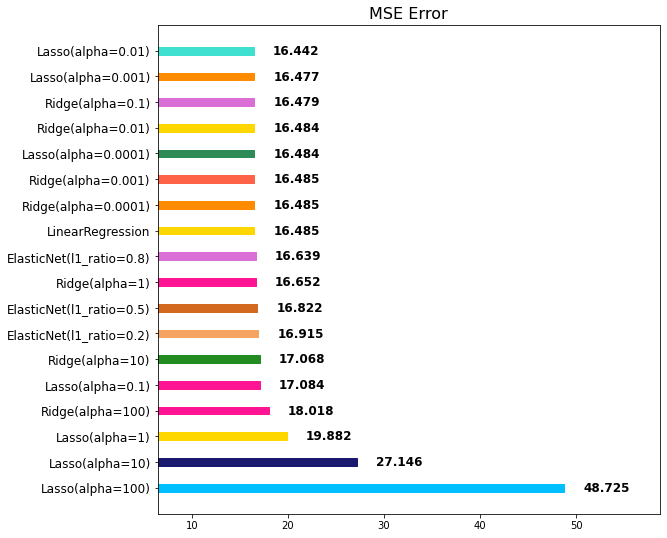
elsticnet_20 = ElasticNet(alpha=5, l1_ratio=0.2) # l2에 비중 크게
elsticnet_20.fit(x_train, y_train)
elasticnet_pred_20 = elsticnet_20.predict(x_test)
elsticnet_80 = ElasticNet(alpha=5, l1_ratio=0.8) # l1에 비중 크게
elsticnet_80.fit(x_train, y_train)
elasticnet_pred_80 = elsticnet_80.predict(x_test)
plot_coef(x_train.columns, elsticnet_20.coef_)
- alpha(규제 강도)=5, L2 비중 크게
컬럼 중 가중치가 가장 컸던 NOX의 중요도가 0인 것을 보면 학습이 안 된 것과 같습니다.
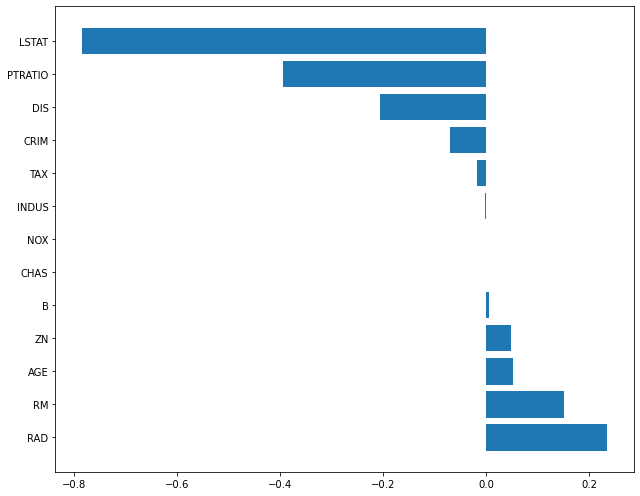
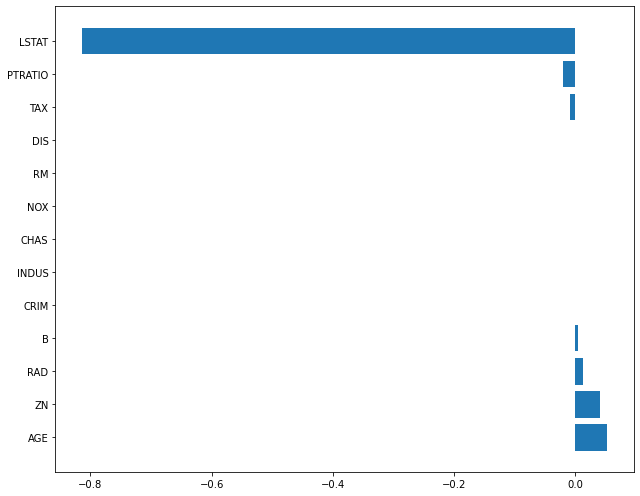
- alpha(규제 강도)=5, L1 비중 크게
plot_coef(x_train.columns, elsticnet_80.coef_)
Scaler 적용
데이터 전처리 과정에서 scaling 방법으로 표준화, 정규화 방법이 있었습니다.
규제 강도를 조절하여도 좋은 성능을 내지 못 하는 경우 데이터의 scale를 변경하는 방법도 고려해야 합니다.
from sklearn.preprocessing import MinMaxScaler, StandardScaler
MinMaxScaler (정규화)
정규화 (Normalization)도 표준화와 마찬가지로 데이터의 스케일을 조정합니다.
정규화가 표준화와 다른 가장 큰 특징은 모든 데이터가 0 ~ 1 사이의 값을 가집니다.
즉, 최대값은 1, 최소값은 0으로 데이터의 범위를 조정합니다.
minmax_scaler = MinMaxScaler()
minmax_scaled = minmax_scaler.fit_transform(x_train)
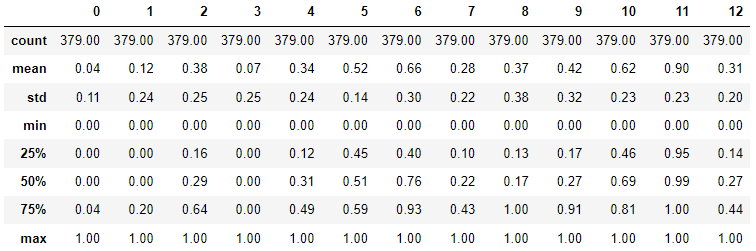
min값과 max값을 0~1 사이로 정규화
minmax_scaler = MinMaxScaler()
minmax_scaled = minmax_scaler.fit_transform(x_train)
round(pd.DataFrame(minmax_scaled).describe(), 2)
StandardScaler (표준화)
표준화는 데이터의 평균을 0 분산 및 표준편차를 1로 만들어 줍니다.
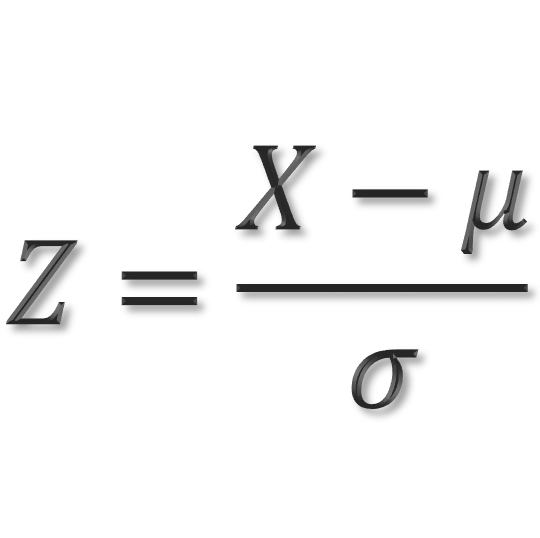
표준화를 하는 이유
- 서로 다른 통계 데이터들을 비교하기 용이하기 때문입니다.
- 표준화를 하면 평균은 0, 분산과 표준편차는 1로 만들어 데이터의 분포를 단순화 시키고, 비교를 용이하게 합니다.
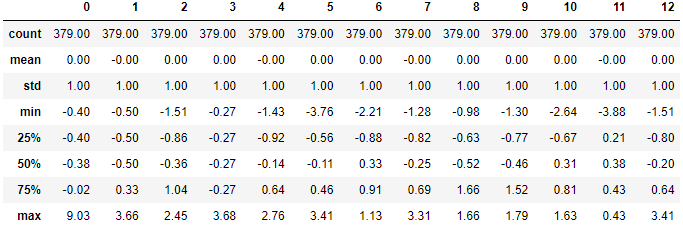
std_scaler = StandardScaler()
std_scalerd = std_scaler.fit_transform(x_train)
round(pd.DataFrame(std_scalerd).describe(), 2)
파이프라인 (pipeline)
scikit-learn의 전처리(pre-processing)용 모듈과 모델의 학습 기능을 파이프라인으로 합칠 수 있습니다.
- 파이프라인으로 결합된 모형은 원래의 모형이 가지는 fit, predict 함수를 가집니다.
- 파이프라인에 정의된 순서에 따라 전처리 모듈이 먼저 호출되어 전처리 과정을 거친 후 모델이 학습하게 됩니다.
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(
MinMaxScaler(),
ElasticNet(alpha=0.1, l1_ratio=0.2) # L2를 강하게 쓰겠다
)
pipeline.fit(x_train, y_train)
pipeline_pred = pipeline.predict(x_test)
mse_eval('MinMax ElasticNet', pipeline_pred, y_test)
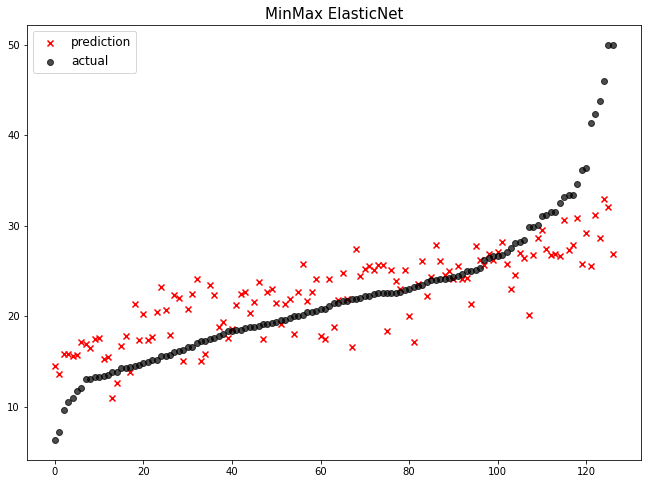
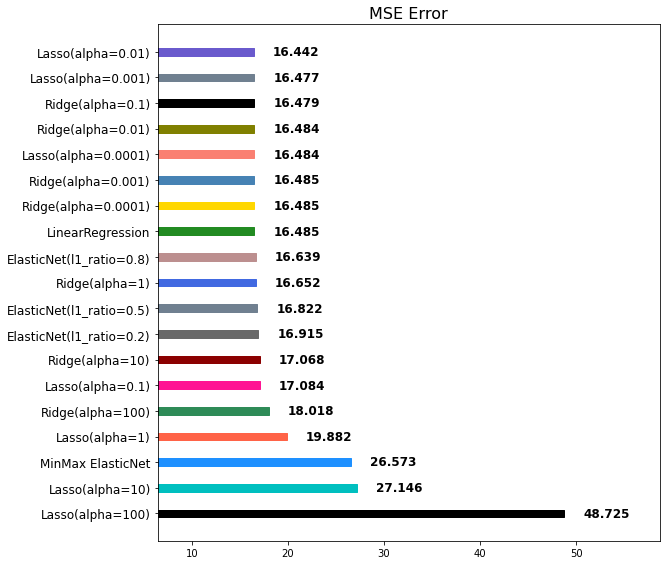
위의 그래프 순위를 보면 MinMax ElasticNet이 아래에서 세 번째로 랭크되었습니다.
따라서 현재 다루고 있는 데이터에는 MinMax와 ElasticNet는 동시에 사용하는 방식이 맞지 않는 것이라고 할 수 있습니다.
pipeline = make_pipeline(
StandardScaler(),
ElasticNet(alpha=0.1, l1_ratio=0.2)
)
pipeline.fit(x_train, y_train)
pipeline_pred = pipeline.predict(x_test)
mse_eval('Standard ElasticNet', pipeline_pred, y_test)
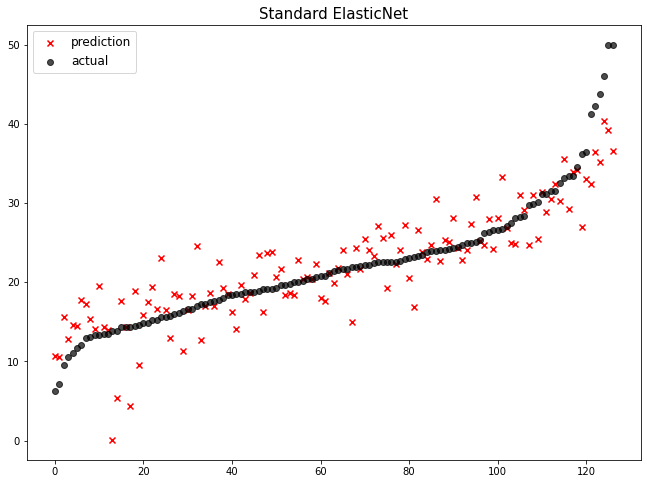
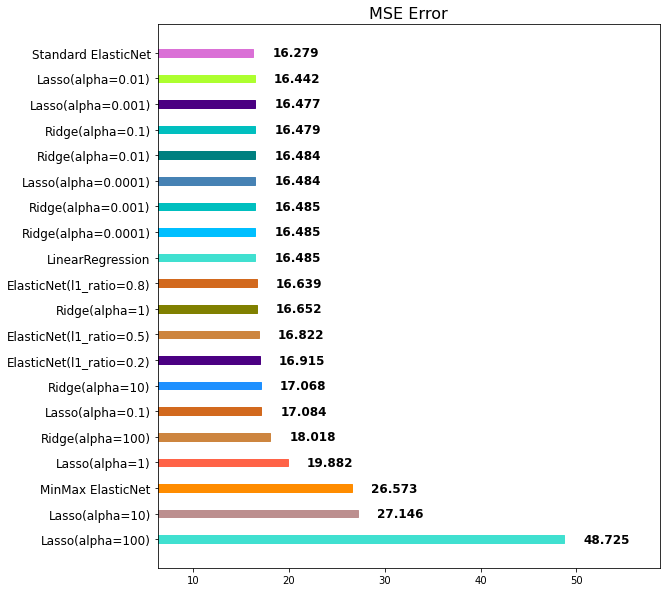
Standard ElasticNet이 1위에 랭크된 것을 보아서 StandardScaler와 ElasticNet을 함께 적용하면 현재 다루고 있는 데이터에서 성능을 가장 좋게 낸다고 할 수 있습니다.
Polynomial Features
- 연속형 레이블과 특성 간의 관계가 선형이 아닌 경우 1차식으로 표현이 불가능하여 2차식 이상의 다항식으로 변형하여 회귀 분석을 진행해야 함
- 기존의 특성에 다항을 적용하여 새로운 특성을 추가
- scikit-learn의 경우 PolynomialFeatures 객체를 이용하여 다항 변환 및 상호교차항을 쉽게 추가 기능
다항식의 계수간 상호작용을 통해 새로운 feature를 생성합니다.
예를들면, [a, b] 2개의 feature가 존재한다고 가정하고,
degree=2로 설정한다면, polynomial features 는 [1, a, b, a^2, ab, b^2] 가 됩니다.
주의
- degree를 올리면, 기하급수적으로 많은 feature 들이 생겨나며, 학습 데이터에 지나치게 과대적합 될 수 있습니다.
주요 hyperparameter
- degree: 차수
- include_bias: 1로 채운 컬럼 추가 여부
- interaction_only : 상호교차항만 반환 유무(False)
# 차수를 2로 하면 제곱이 된다.
# 1은 새로운 값의 창줄이 아니라 default 상수값이라 학습에 도움지 되지 않는다..!
from sklearn.preprocessing import PolynomialFeatures
x = np.arange(5).reshape(-1,1)
x
'''
array([[0],
[1],
[2],
[3],
[4]])
'''
degree=2, include_bias=False 인 경우
# degree 옵션은 각각 제곱 나오고, 원래 값 나오고, include=False
poly = PolynomialFeatures(degree=2, include_bias=False)
x_poly = poly.fit_transform(x)
x_poly
'''
array([[ 0., 0.],
[ 1., 1.],
[ 2., 4.],
[ 3., 9.],
[ 4., 16.]])
'''
degree=2, include_bias=True 인 경우
poly = PolynomialFeatures(degree=2, include_bias=True) # 1 추가된 것일뿐
x_poly = poly.fit_transform(x)
x_poly
'''
array([[ 1., 0., 0.],
[ 1., 1., 1.],
[ 1., 2., 4.],
[ 1., 3., 9.],
[ 1., 4., 16.]])
'''
degree=3, include_bias=True 인 경우
poly = PolynomialFeatures(degree=3, include_bias=True) # 1 추가된 것일뿐
x_poly = poly.fit_transform(x)
x_poly
'''
array([[ 1., 0., 0., 0.],
[ 1., 1., 1., 1.],
[ 1., 2., 4., 8.],
[ 1., 3., 9., 27.],
[ 1., 4., 16., 64.]])
'''
poly = PolynomialFeatures(degree=3, include_bias=False)
x_poly = poly.fit_transform(x)
x_poly
# 칼럼 간 종합적인 정보를 추출한다
'''
array([[ 0., 0., 0.],
[ 1., 1., 1.],
[ 2., 4., 8.],
[ 3., 9., 27.],
[ 4., 16., 64.]])
'''
보스턴 집 값 데이터의 features에 PolynomialFeatures를 적용합니다.
poly = PolynomialFeatures(degree=2, include_bias=False)
poly_features = poly.fit_transform(x_train)
x_train.shape # (379, 13) 칼럼의 개수13개
poly_features.shape # (379, 104) => 통합정보 칼럼 생성으로 개수 늘어남!
PolynomialFeature로 증폭시킨 칼럼을 다시 전처리 과정을 거치는 것은 너무 비효율적인 작업
PolynomialFeature도 파이프라인(pipeline)을 활용하여 전처리 해준다면, 손쉽게 구현 및 적용이 가능합니다.
poly_pipeline = make_pipeline(
PolynomialFeatures(degree=2, include_bias=False),
ElasticNet(alpha=0.1, l1_ratio=0.2)
)
poly_pipeline.fit(x_train, y_train)
poly_pred = poly_pipeline.predict(x_test)
mse_eval('Poly ElasticNet', poly_pred, y_test)
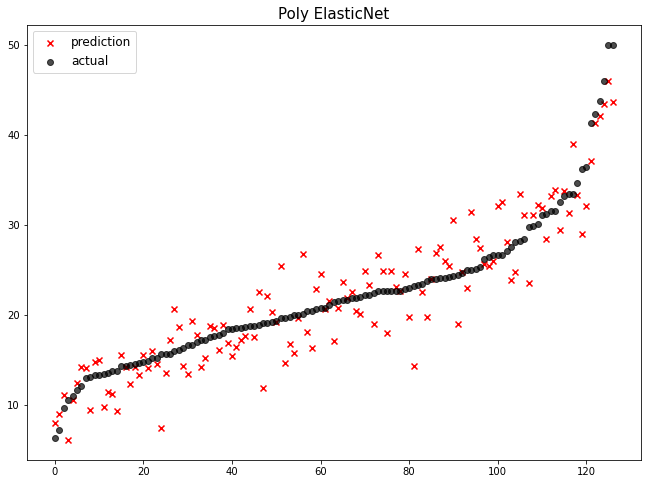
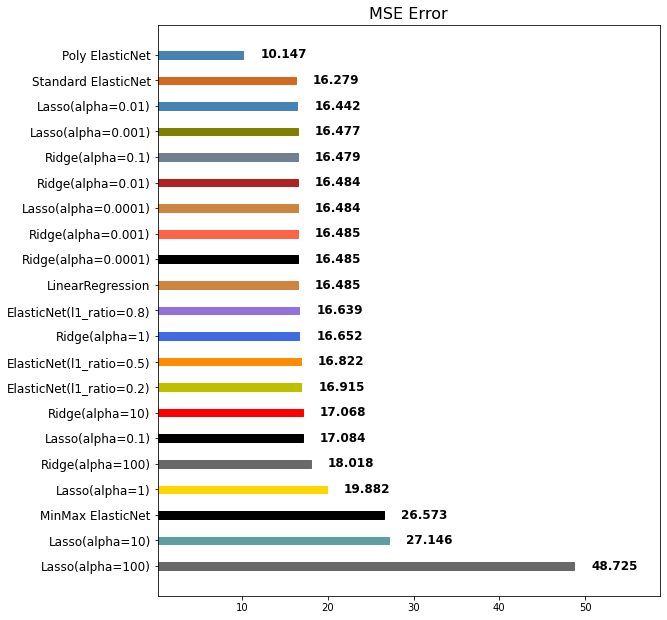
Poly ElasticNet이 1위로 랭크된 것을 보아 PolynomialFeatures과 ElasticNet 모델을 함께 적용하면 현재 데이터에서 좋은 예측 성능을 보임을 알 수 있습니다.
poly_pipeline = make_pipeline(
StandardScaler(),
PolynomialFeatures(degree=2, include_bias=False),
ElasticNet(alpha=0.1, l1_ratio=0.2)
)
poly_pipeline.fit(x_train, y_train)
poly_pred = poly_pipeline.predict(x_test)
mse_eval('Poly, Standard ElasticNet', poly_pred, y_test)
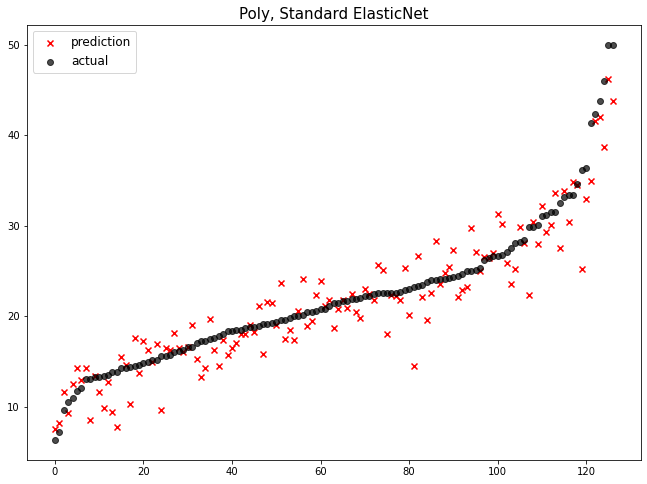
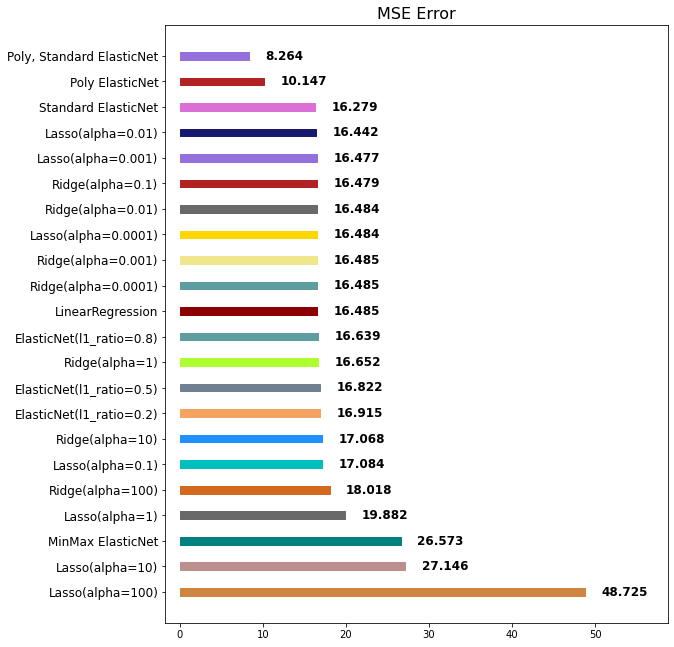
StandardScaler과 PolynomialFeatures과 ElasticNet 모델을 함께 사용했을 때 현재 데이터에서 성능이 가장 좋음을 알 수 있습니다.
'AI > 머신러닝' 카테고리의 다른 글
| [머신러닝] 결정트리 (0) | 2022.04.18 |
|---|---|
| [머신러닝] 로지스틱 (0) | 2022.04.16 |
| [머신러닝] 회귀 모델 (Regression Models) 1 (0) | 2022.04.16 |
| [머신러닝] 경사하강법 (Gradient Descent) 2 (0) | 2022.04.16 |
| [머신러닝] 경사하강법 (Gradient Descent) 1 (0) | 2022.04.16 |




댓글