결정트리 or 의사결정나무 (Decision Tree)
결정트리를 가장 단수하게 표현하자면, Tree 구조를 가진 알고리즘입니다.
의사결정나무는 데이터를 분석하여 데이터 사이에서 패턴을 예측 가능한 규칙들의 조합으로 나타내며, 이 과정을 시각화 해 본다면 마치 스무고개 놀이와 비슷합니다.
의사 결정트리는 의사를 어떻게 결정할지에 따라 다른 결과를 도출하는 방식으로 전개된다.트리란 내가 의사를 결정하는데 있어서 선택지가 2가지만 있는 것이 아니라 여러 개의 선택지 가능하고 나무를 뒤집어 놓은 것처럼, 가지에 가지를 뻗은 행태로 의사를 결정해 나가는 구조라서 트리라는 이름이 붙여졌다.
이렇게 가지를 뻗어나가는 형태로 최종 의사를 결정할 수 있다.

질문을 던지면서 범위를 축소시켜 나간다.
가장 위의 ‘날개가 있나요?’ 질문은 RootNode라고 함 맨 마지막 매, 펭귄, 돌고래, 곰은 LeafNode라고 한다.
한 칸씩 내려올 때 depth 1, depth 2로 명칭한다.
우리가 가지고 있는 컬럼으로 질문(의사)를 만들자. 이 질문을 어떤 알고리즘으로 생성하느냐?
의사결정나무는 classification과 regression 방식 두 가지가 있다.
질문을 creating 할 때 classification 방식(지느러미가 있나요? yes/no)와 regression(돈이 100만원 이상 있나요? 어느정도 범위.. 150만원)

1번째 depth에서 무조건 아래처럼 분류함

처음 붉은 색과 파란 색이 50:50으로 나뉨. 컬럼의 두 번째 값 (인덱스 1)이 0.0596보다 작거나 같나요?
counts = [2,32] ⇒ 파란색 2개, 붉은색 32개
counts = [48,18] ⇒ 숫자는 서로 다른 클래스의 개수
하나의 영역 안에 되도록 하나의 클래스가 들어가는 것이 순도가 높다.
따라서 좋은 질문은 counts = [2,32] 가 된다.

밑에 영역에서 선 하나를 더 그었다. ⇒ 새로운 질문을 생성한 것이다.
첫 번째 값이 0.4377보다 작거나 같나요?
depth 두 단계 만에 순수 pure한 노드로 분류해낼 수 있었다.
⇒ 질문의 컬럼을 추천하는 최고의 우선순위는?
불순도를 낮추는 방향으로 질문을 생성한다. 어떤 컬럼을 뽑아서 어떤 질문을 해야 하나의 영역에 하나의 클래스가 들어가는가. 모든 컬럼을 대조하여 최적의 칼럼을 찾아낸다.
오른쪽 상단에 파란 원 하나가 눈에 띄지만 overfitting 될 수 있으니 그냥 두자..

그럼에도 불구하고 오른쪽 상단의 파란 원을 구출해 낸다!
decision tree는 성능이 좋고 직관적이다.
모든 칼럼을 가지고 불순도를 줄일 수 있도록 한다.
decision tree의 취약점? Overfitting
어느 정도에서 가지치기로 질문 그만 던지게끔 합니다.
결정트리의 기본 아이디어는 sample이 가장 섞이지 않은 상태로 완전히 분류되는 것, 다시 말해서 엔트로피(Entropy)를 낮추도록 만드는 것입니다.
불순도(얼마나 섞여있냐) ⇒ 엔트로피 지수
엔트로피 (Entropy)
엔트로피는 쉽게 말해서 무질서한 정도를 정량화(수치화)한 값입니다.
다음은 엔트로피 지수를 불순도에 따른 지표로 표현되었습니다.

결정트리에서 질문을 만들어내는 기준은 불순도를 최소화하는 방향으로 결정되어진다불순도란 해당 범주 안에 서로 다른 데이터가 얼마나 섞여 있는지를 말하는데트리의 아랫 부분으로 내려 갈수록 불순도가 낮아진다.곧 순도가 높아지는 방향이다.
한범주에 서로 다른 데이터가 1일 때 불순도가 가장 낮고한 범주 안에 서로 다른 데이터가 정확히 반반 있다면 불순도가 가장 높다
엔트로피는 무질서함(불순도)을 나타내는 지표이고엔트로피 계수를 그대로 변환해서 사용하는 것이 지니계수(지니계수는 엔트로피계수를 변형시킨 것)이다. 결정트리에서 사용되는 지니 계수는 0~0.5사이의 값을 가진다. 0.5(50:50으로 불순도 가장 높음)
50:50일 때 불순도가 높다
1:49일 때 순도가 높다
엔트로피 수식의 이해
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 샘플데이터를 생성합니다.
group_1 = np.array([0.3, 0.4, 0.3])
group_2 = np.array([0.7, 0.2, 0.1])
group_3 = np.array([0.01, 0.01, 0.98])
fig, axes = plt.subplots(1, 3)
fig.set_size_inches(12, 4)
axes[0].bar(np.arange(3), group_1, color='blue')
axes[0].set_title('Group 1')
axes[1].bar(np.arange(3), group_2, color='red')
axes[1].set_title('Group 2')
axes[2].bar(np.arange(3), group_3, color='green')
axes[2].set_title('Group 3')
plt.show()


# entropy를 python으로 구현합니다.
def entropy(x):
return -(x * np.log2(x)).sum()
Entropy 계산 및 시각화
# 불순도를 측정하는 지수
entropy_1 = entropy(group_1)
entropy_2 = entropy(group_2)
entropy_3 = entropy(group_3)
print(f'Group 1: {entropy_1:.3f}\\nGroup 2: {entropy_2:.3f}\\nGroup 3: {entropy_3:.3f}')
'''
Group 1: 1.571
Group 2: 1.157
Group 3: 0.161
'''

지니 계수 (Gini Index)
- 클래스들이 공평하게 섞여 있을 수록 지니 계수는 올라갑니다.
- Decision Tree는 지니 불순도를 낮추는 방향으로 가지치기를 진행합니다.
# Gini Index 구현합니다.
def gini(x):
return 1 - ((x / x.sum())**2).sum()
# 샘플데이터를 생성합니다.
group_1 = np.array([50, 50]) # 불순도 최고
group_2 = np.array([30, 70])
group_3 = np.array([0, 100]) # 순도 100
fig, axes = plt.subplots(1, 3)
fig.set_size_inches(12, 4)
axes[0].bar(['Positive', 'Negative'], group_1, color='blue')
axes[0].set_title('Group 1')
axes[1].bar(['Positive', 'Negative'], group_2, color='red')
axes[1].set_title('Group 2')
axes[2].bar(['Positive', 'Negative'], group_3, color='green')
axes[2].set_title('Group 3')
plt.show()

gini_1 = gini(group_1)
gini_2 = gini(group_2)
gini_3 = gini(group_3)
print(f'Group 1: {gini_1:.3f}\\nGroup 2: {gini_2:.3f}\\nGroup 3: {gini_3:.3f}')
# 지니 지수는 0~0.5 범위이다!
'''
Group 1: 0.500
Group 2: 0.420
Group 3: 0.000
'''
plt.figure(figsize=(5, 5))
plt.bar(['Group 1', 'Group 2', 'Group 3'], [gini_1, gini_2, gini_3])
plt.title('Gini Index', fontsize=15)
plt.show()

Decision Tree 구현
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
SEED = 42
# train_test_split 데이타 분할
x_train, x_test, y_train, y_test = train_test_split(cancer['data'], cancer['target'], stratify=cancer['target'], random_state=SEED)
# breast cancer 데이타셋 로드
cancer = load_breast_cancer()
# train_test_split 데이타 분할
x_train, x_test, y_train, y_test = train_test_split(cancer['data'], cancer['target'], stratify=cancer['target'], random_state=SEED)
# 알고리즘(모델) 정의
tree = DecisionTreeClassifier(random_state=0)
# 학습
tree.fit(x_train, y_train)
# 예측
pred = tree.predict(x_test)
# 정확도 측정
accuracy = accuracy_score(pred, y_test)
print(f'Accuracy Score: {accuracy:.3f}') # Accuracy Score: 0.937
의사결정나무의 시각화
import graphviz
from sklearn.tree import export_graphviz
def show_trees(tree):
export_graphviz(tree, out_file='cancer_tree.dot',
class_names=cancer.target_names,
feature_names=cancer.feature_names,
#impurity=False, # gini 미출력
impurity=True, # gini 계수 같이 보기
filled=True)
with open('cancer_tree.dot', encoding='utf-8') as f:
dot_graph = f.read()
# display(graphviz.Source(dot_graph)) # PATH 설정 후 주석 풀어줄게!
show_trees(tree)
장점
쉽고 직관적입니다.각 피처의 스케일링과 정규화 같은 전처리 작업의 영향도가 크지 않습니다.
단점
규칙을 추가하며 서브트리를 만들어 나갈수록 모델이 복잡해지고, 과적합에 빠지기 쉽습니다.→ 트리의 크기를 사전에 제한하는 하이퍼파라미터 튜닝(pruning 처리, 가지치기 처리 해줘야 함)이 필요합니다.

주요 Hyper Parameter
max_depth
max_depth는 최대 트리의 깊이를 제한 합니다. max_depth=4 이면 그 밑에 다 잘라냄.
기본 값은 None, 제한 없음 입니다.
min_sample_split
min_sample_split 노드 내에서 분할이 필요한 최소의 샘플 숫자입니다. 하나의 노드에 들어갈 샘플을 제한합니다. (default 2)
tree = DecisionTreeClassifier(max_depth=3, random_state=SEED)
tree.fit(x_train, y_train)
show_trees(tree)
# dot 파일 다시 복사해서 web graph 가!

tree = DecisionTreeClassifier(max_depth=6, min_samples_split=20, random_state=SEED)
tree.fit(x_train, y_train)
show_trees(tree)

지니 계수가 0.0이라서 더 이상 분기하지 않아도 됨
max_depth가 6이라 6단계 이상으로 더 이상 분기하지 않음 어차피 max_depth가 6이었다..
max_leaf_nodes
max_leaf_nodes는 말단 노드의 최대 갯수 (과대 적합 방지용)
기본 값은 None, 제한 없음 입니다.
tree = DecisionTreeClassifier(max_leaf_nodes=10, random_state=SEED)
tree.fit(x_train, y_train)
show_trees(tree)

max_features
최적의 분할을 찾기 위해 고려할 피처의 수
0.8 은 80% 의 feature 만 고려하여 분할 알고리즘 적용
기본 값은 None, 모두 사용입니다.

의사 결정 나무가 만들어지면 내부적으로 model의 coef, intersection?? 두 속성이 자동으로 만들어짐
이와 같이 feature도 자동으로 변수를 반들어냄
어떤 컬럼을 중요하게 삼는지..
feature의 중요도
feature_importances_ 변수를 통해서 tree 알고리즘이 학습시 고려한 feature 별 중요도를 확인할 수 있습니다.
결정트리 모델을 생성하고 수행하게되면 결과적으로 속성의 중요도를 알 수 있는 특성 중요도 인스턴스가 생성된다.
결정트리를 만드는데 있어서어떤 의사결정, 조건, 질문, 특징, 속성으로 결정되는가...다 같은 말이다.
특성 중요도는Tree모델을 생성해서 학습시키고 난후, 내부적으로 생성되는 인스턴스이다.
트리구조상 상위에 있는 특성, 속성이 중요한 것으로 지정되며트리계층을 내려갈수록 중요도가 떨어지는데, 그렇다고 이것이 필요없는 속성으로 바로 간주하는 것은위험한 발상이다.
특성 중요도는 트리의 계층구조와 밀접한 연관을 가진다.
tree.feature_importances_
'''
array([0. , 0. , 0. , 0. , 0.00752597,
0. , 0. , 0.01354675, 0. , 0. ,
0. , 0.05383566, 0. , 0.00238745, 0.00231135,
0. , 0. , 0. , 0. , 0. ,
0.69546322, 0.04179055, 0. , 0. , 0.00668975,
0. , 0.01740312, 0.12587473, 0.02341413, 0.00975731])
'''
0은 의사결정 할 때 사용되지 않는 컬럼을 나타낸다.
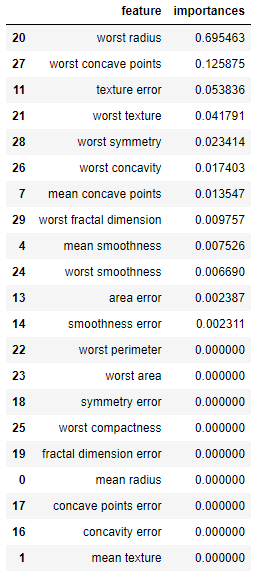
DataFrame으로 만들면 중요도(feature importances) 순서로 정렬할 수 있습니다.
import pandas as pd
# 컬럼당 importances 나옴
df = pd.DataFrame(list(zip(cancer['feature_names'], tree.feature_importances_)),
columns=['feature', 'importances']).sort_values(by='importances', ascending=False)
df
의사 결정 시 Entropy 지수가 가장 낮게 나오는 방향으로 결정
관련된 칼럼을 채택해서 질문을 생성한다. 이때 가장 엔트로피 지수를 낮출 수 있는 칼럼이 가장 위에 랭크된 컬럼이다. 따라서 가장 위의 worst radius가 루트 노드가 됨
특성 중요도 시각화
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10,10))
sns.barplot(y='feature', x='importances', data=df)
plt.show()

'AI > 머신러닝' 카테고리의 다른 글
| [머신러닝] Ensemble (앙상블) (0) | 2022.04.18 |
|---|---|
| [머신러닝] Ensemble (앙상블) (0) | 2022.04.18 |
| [머신러닝] 로지스틱 (0) | 2022.04.16 |
| [머신러닝] 회귀 모델 (Regression Models) 2 (0) | 2022.04.16 |
| [머신러닝] 회귀 모델 (Regression Models) 1 (0) | 2022.04.16 |




댓글