본문 바로가기
AI/머신러닝

[머신러닝] 경사하강법 (Gradient Descent) 2

by snow_white 2022. 4. 16.

샘플에 활용할 데이터 셋 만들기

from IPython.display import Image
import numpy as np
import matplotlib.pyplot as plt

def make_linear(w=0.5, b=0.8, size=50, noise=1.0): # 노이즈 거의 없음
    x = np.random.rand(size)
    y = w * x + b
    noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
    yy = y + noise
    plt.figure(figsize=(10, 7))
    plt.plot(x, y, color='r', label=f'y = {w}*x + {b}')
    plt.scatter(x, yy, label='data')
    plt.legend(fontsize=20)
    plt.show()
    print(f'w: {w}, b: {b}')
    return x, yy
x, y = make_linear(w=0.3, b=0.5, size=100, noise=0.01)

plt.figure(figsize=(10, 7))
plt.scatter(x, y)
plt.show()

파란색=실제 데이터, 빨간색=예측

 

초기값 (Initializer)과 y_hat (예측, prediction) 함수 정의

w, b 값에 대하여 random한 초기 값을 설정해 줍니다.

이전에 LinearRegression은 MSE 방식으로 예측했다면 이번에는 경사하강법으로 선형 회귀를 예측해봅시다.

w = np.random.uniform(low=-1.0, high=1.0)
b = np.random.uniform(low=-1.0, high=1.0)
w, b # (0.24576366211925782, -0.0905235096930701)

 

y_hat은 prediction 값 입니다. 즉, 가설함수에서 실제 값 (y)를 뺀 함수를 정의합니다.

# Hypothesis 함수 정의 H(x)
y_hat = w * x + b
y_hat
'''
array([ 0.04868998,  0.07284164, -0.01250057, -0.02794568, -0.08377864,
        0.059778  , -0.01477152, -0.05601984,  0.05234526,  0.03133528,
'''

 

Gradient Descent 구현 (1. 단항식)

num_epoch = 5000 # 학습 횟수

learning_rate = 0.5

errors = []

w = np.random.uniform(low=-1.0, high=1.0)
b = np.random.uniform(low=-1.0, high=1.0)

for epoch in range(num_epoch):
        
       
    # 경사하강법 미분 계산..w를 보정하면서 산을 내려온다
    # 먼저 예측을 하고
    y_hat = w * x + b
    # loss(error) 계산하고
    error = ((y_hat - y)**2).mean()
    # 평지 근처에 오면 stop
    if error < 0.0005:
        break
    # 아니면 값 보정
    w = w-learning_rate*((y_hat-y) * x).mean()
    b = b-learning_rate*(y_hat-y).mean()
    
    errors.append(error)
    
    if epoch % 5 == 0:
        print("{0:2} w = {1:.5f}, b = {2:.5f} error = {3:.5f}".format(epoch, w, b, error))
    
print("----" * 15)
print("{0:2} w = {1:.1f}, b = {2:.1f} error = {3:.5f}".format(epoch, w, b, error))
'''
 0 w = -0.03524, b = 0.80031 error = 0.13066
 5 w = -0.02752, b = 0.66551 error = 0.00950
10 w = 0.02282, b = 0.63921 error = 0.00677
15 w = 0.06566, b = 0.61772 error = 0.00483
20 w = 0.10182, b = 0.59960 error = 0.00345
25 w = 0.13234, b = 0.58431 error = 0.00246
30 w = 0.15809, b = 0.57140 error = 0.00176
35 w = 0.17983, b = 0.56050 error = 0.00126
40 w = 0.19817, b = 0.55131 error = 0.00091
45 w = 0.21365, b = 0.54355 error = 0.00066
--------------------------------------------
50 w = 0.2, b = 0.5 error = 0.00048
'''

 

시각화

학습 진행(epoch)에 따른 오차를 시각화 합니다.

plt.figure(figsize=(10, 7))
plt.plot(errors)
plt.xlabel('Epochs')
plt.ylabel('Error')
plt.show()

학습이 진행됨에 다른 error율

learning rate를 0.0005로 작게하면 보폭이 작아서 내려오기도 전에 5000번 학습이 끝나버립니다.

4990 w = 1.02938, b = 0.07659 error = 0.05101
4995 w = 1.02933, b = 0.07680 error = 0.05097
----------------------------------------------
4999 w = 1.0, b = 0.1 error = 0.05094

learning rate 를 5.5 로 줬을 때 발산하기 때문에 오차가 너무 커서 W, bias 값이 커지다가 더 이상 계산이 안 되는 값이 됩니다. ⇒ 오차가 너무 커서 계산할 수 없어서 Nan을 출력합니다.

 

Gradient Descent 구현 (2. 다항식)

 

샘플 데이터를 생성합니다.

이번에는 Feature Data, 즉 X 값이 여러 개인 다항식의 경우에 대해서도 구해보도록 하겠습니다.

다항식에서는 X의 갯수 만큼, W 갯수도 늘어날 것입니다. feature값이 여러 개면 W값도 feature 개수만큼 늘어나야 합니다. 

다만, bias (b)의 계수는 1개인 점에 유의해 주세요.

x1 = np.random.rand(100)
x2 = np.random.rand(100)
x3 = np.random.rand(100)

w1 = np.random.uniform(low=0.0, high=1.0)
w2 = np.random.uniform(low=0.0, high=1.0)
w3 = np.random.uniform(low=0.0, high=1.0)

b = np.random.uniform(low=0.0, high=1.0)

 

w1, w2, w3, b  다항식을 정의합니다.

# 정답값을 미리 세팅해 놓자. w1, w2, w3, b
y = 0.3 * x1 + 0.5 * x2 + 0.7 * x3 + 0.9

Gradient Descent 구현 (다항식)

errors = []
w1_grad = []
w2_grad = []
w3_grad = []

num_epoch=5000
learning_rate=0.5

w1 = np.random.uniform(low=0.0, high=1.0)
w2 = np.random.uniform(low=0.0, high=1.0)
w3 = np.random.uniform(low=0.0, high=1.0)

b = np.random.uniform(low=0.0, high=1.0)

for epoch in range(num_epoch):
    
   
    # 다항식 Grdien Descent
    # 예측값
    y_hat = w1 * x1 + w2 * x2 + w3 * x3 +b
    error = ((y_hat-y)**2).mean()
    errors.append(error)
    if error < 0.00001:
        break
    
    # 계속 하강하도록.. 편미분
    w1 = w1 - learning_rate * ((y_hat-y)*x1).mean()
    w2 = w2 - learning_rate * ((y_hat-y)*x2).mean()
    w3 = w3 - learning_rate * ((y_hat-y)*x3).mean()
    
    b = b-learning_rate * (y_hat-y).mean()
    
    w1_grad.append(w1)
    w2_grad.append(w2)
    w3_grad.append(w3)

    if epoch % 5 == 0:
        print("{0:2} w1 = {1:.5f}, w2 = {2:.5f}, w3 = {3:.5f}, b = {4:.5f} error = {5:.5f}".format(epoch, w1, w2, w3, b, error))
    
print("----" * 15)
print("{0:2} w1 = {1:.1f}, w2 = {2:.1f}, w3 = {3:.1f}, b = {4:.1f} error = {5:.5f}".format(epoch, w1, w2, w3, b, error))
'''140 w1 = 0.31008, w2 = 0.50159, w3 = 0.70729, b = 0.89015 error = 0.00001
------------------------------------------------------------
145 w1 = 0.3, w2 = 0.5, w3 = 0.7, b = 0.9 error = 0.00001
'''
# 시각화
plt.figure(figsize=(10, 7))
plt.plot(errors)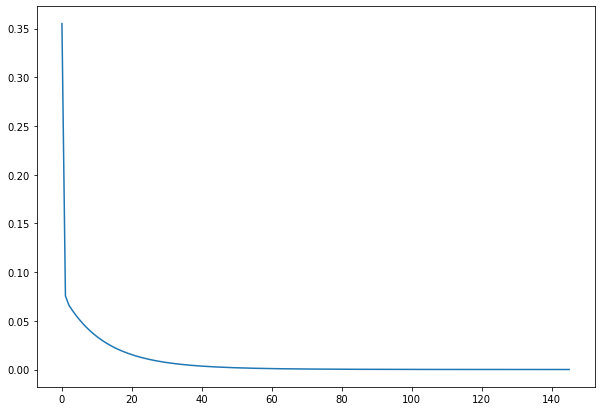

 

가중치 (W1, W2, W3) 값들의 변화량 시각화

Epoch가 지남에 따라 어떻게 가중치들이 업데이트 되는지 시각화 해 봅니다.

 

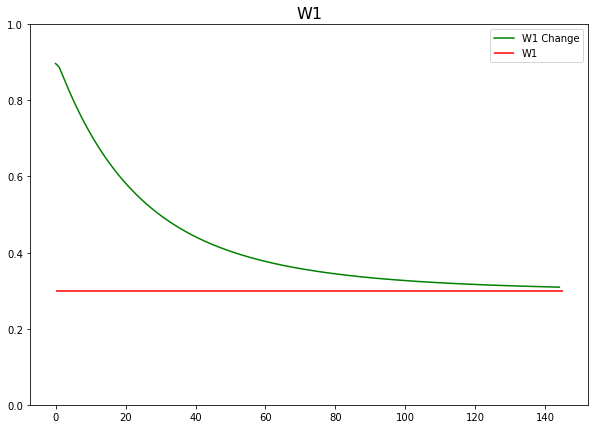
  • W1 가중치 보정되는 과정
plt.figure(figsize=(10, 7))

plt.hlines(y=0.3, xmin=0, xmax=len(w1_grad), color='r')
plt.plot(w1_grad, color='g')
plt.ylim(0, 1)
plt.title('W1', fontsize=16)
plt.legend(['W1 Change', 'W1'])
plt.show()

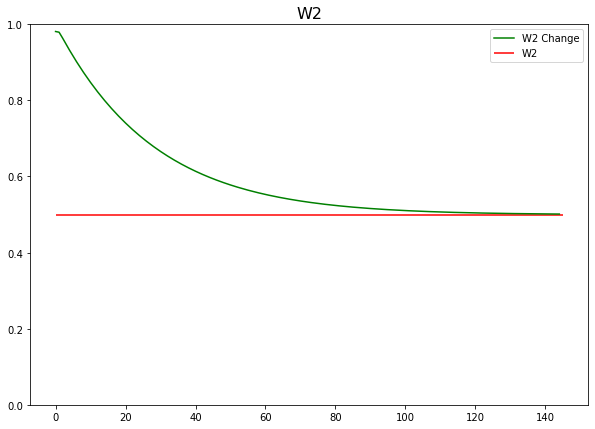
  • W2 가중치 보정되는 과정
plt.figure(figsize=(10, 7))

plt.hlines(y=0.5, xmin=0, xmax=len(w2_grad), color='r')
plt.plot(w2_grad, color='g')
plt.ylim(0, 1)
plt.title('W2', fontsize=16)
plt.legend(['W2 Change', 'W2'])
plt.show()

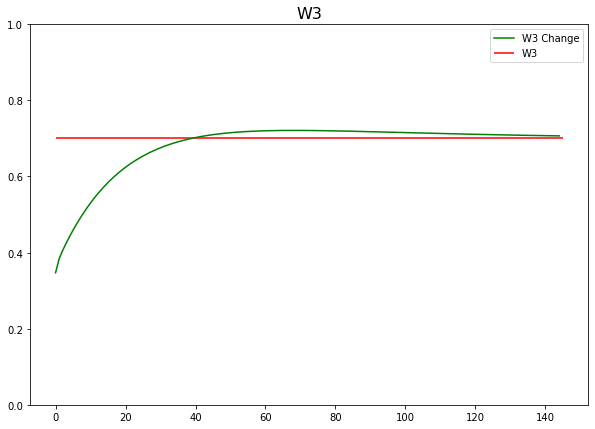
  • W3 가중치 보정되는 과정
plt.figure(figsize=(10, 7))

plt.hlines(y=0.7, xmin=0, xmax=len(w3_grad), color='r')
plt.plot(w3_grad, color='g')
plt.ylim(0, 1)
plt.title('W3', fontsize=16)
plt.legend(['W3 Change', 'W3'])
plt.show()

 

  • 최소제곱법 ⇒ 내부적으로 sklearn.Linear 모델 모듈에서는 linear regression 모델 제공
  • 경사하강법 ⇒ 내부적으로 sklearn.Linear 모델 모듈 안에서는  SGDregression 모델 제공

 

경사하강법을 활용한 SGDRegressor

linear 모델이기 때문에 linear_model import 해야 합니다.

from sklearn.linear_model import SGDRegressor
model = SGDRegressor(max_iter=5000, tol=1e-5, learning_rate='constant') # epoch 5000번 학습

# model.fit(x,y) => series라서 reshape 필수
x1 = x1.reshape(-1,1)
x2 = x2.reshape(-1,1)
x3 = x3.reshape(-1,1)

x1.shape # (100, 1)

# 위 세 개의 칼럼을 하나로 묶어주기
X = np.concatenate([x1, x2, x3], axis=1)
X.shape # (100, 3)
model.fit(X,y) # 학습!
# SGDRegressor(learning_rate='constant', max_iter=5000, tol=1e-05) # 5000번 학습, 0.00005보다 loss가 작으면 멈추라는 속성

# 학습이 끝나면 학습의 주체를 데이터로 뽑아오는 것이 목표, 각각의 칼럼에 대한 가중치를 알아야 함
# 전체적인 칼럼의 가중치도 알면 좋음
model.coef_ # 각 feature의 중요도, 따라서 칼럼 개수와 같게 출력됨
# array([0.15502445, 0.15502445, 0.15502445])

# 각각 칼럼에 대한 가중치가 아니라 전체에 대한 편향을 보자
model.intercept_ # array([1.43852891])

print("w1 = {:.1f}, w2 = {:.1f}, w3 = {:.1f}, b = {:.1f}".format(model.coef_[0], model.coef_[1], model.coef_[2], model.intercept_[0]))
# w1 = 0.3, w2 = 0.5, w3 = 0.7, b = 0.9

 

 

머신러닝 학습 시 평가지표

  • 분류(classification) 평가지표
    1. 정확도
      • (predict==y).mean() → 예측값과 실제값을 비교해서 일일이 개수세어 평균내기
      • score(X_test, y_test) ⇒ 내부적으로 predict 돌아가기 때문에 알아서 정확도 계산하기
    2. Confusion(혼동) Matrix

 

  • 회귀(regression) 평가지표  (상대적인 예측과 결과 판단 → 야채 값 오차와 아파트 값 오차)
    • R^2
      • 통계에서 많이 쓰임.
      • 실제값 분산 대비 예측값 분산 비율 도출해내는 방법, 아래 MSE, MAE, RMSE와 다른 분산 방식
      • 0~1 사이 숫자 사용, 1에 가가울 수록 좋은 성능, 0에 가까울 수록 안 좋은 성능
      • 가끔 음수가 나온다면 데이터 잘못된 것임!
    • MSE : 오차의 제곱을 모두 더해서 평균내기, 학습에서는 좋지만 상대적이기 때문에 오차가 커지면 불리해짐
    • MAE : 오차의 절댓값을 씌워 모두 더해서 평균내기
    • RMSE : MSE는 제곱하면 값이 커지기 때문에 MSE에 루트를 씌우기, MSE의 오차를 상쇄시킬 수 있음

 

'AI > 머신러닝' 카테고리의 다른 글

[머신러닝] 회귀 모델 (Regression Models) 2  (0) 2022.04.16
[머신러닝] 회귀 모델 (Regression Models) 1  (0) 2022.04.16
[머신러닝] 경사하강법 (Gradient Descent) 1  (0) 2022.04.16
[머신러닝] 최소제곱법을 활용한 LinearRegression  (0) 2022.04.12
[머신러닝] 데이터 전처리 | 표준화, 정규화  (0) 2022.04.12

관련글

댓글

티스토리툴바